Python para engenharia

Arquivo de roteiros e aulas do curso Python para Engenharia com Aplicações

Capítulo 10: Numpy e Matplotlib

Atividade 1: Numpy

Numpy é uma biblioteca de álgebra linear para Python. É uma das principais bibliotecas utilizadas para na engenharia e matemática. Ela é extremamente rápida vistos que seus principais métodos foram compilados em C, desta forma é possível trabalhar com uma quantidade de dados gigantescas em um curto espaço de tempo. Numpy tem um desempenho superior as listas e tuplas, visto que o Python é uma linguagem simples para o usuário, mas muito lenta para o computador. Sendo assim, trabalhando com o numpy estamos trabalhando com o melhor dos dois mundos. Além disso, devido a sua popularidade, o Numpy é um dos blocos de construção de todas as outras bibliotecas de matemática e engenharia, junto com o sympy e o pandas.

Como o Numpy é uma biblioteca de algebra linear. Pode-se dizer que os array de Numpy são essencialmente de duas formas, vetores e matrizes:

Exemplo 1: Criação de vetores e matrizes

Importando a biblioteca:

A documentação de Numpy recomenda que a importação seja feita da seguinte forma:

import numpy as np #A documentação recomenda utilizar np

Primeiro array:

Inicialmente vamos definir uma lista qualquer, e utilizar o método array para converter a lista em um array de Python:

lista = [2,4,6,8,10] #Crio uma lista
array=np.array(lista) #Uso o método array para converter a minha lista para um array de numpy
display(array)
type(array) #Podemos usar o método type e verificar o método

array([ 2, 4, 6, 8, 10])
numpy.ndarray

Array de duas dimensões (Matriz):

Para criar um matriz, ou um array de duas dimensões utilizamos lista de lista.

matriz_identidade=[[1,0,0],[0,1,0],[0,0,1]] #Definindo uma matriz identidade 3x3
np.array(matriz_identidade) #Convertendo a lista de lista em uma array de duas dimensões

array([[1, 0, 0],
[0, 1, 0],
[0, 0, 1]])

Dica: É fácil perceber a dimensão de uma matriz através da quantidade de colchetes (Matriz tem dois colchetes e vetor tem apenas um colchete)

Exemplo 2: Funções de criação de arrays

Função arange:

Com a função arange é possível criar uma sequência de números dentro de um intervalo. Ele tem a seguinte notação:

np.arange(
    inicio,
    fim,
    [passo] # Este último é opcional, o padrão é 1
)
​```
ou:
​```python
np.arange(
    fim
)

Quando utilizamos apenas um argumento, o intervalo retornado é $x\in[0,\text{fim})$, com passo 1.

Vamos criar uma sequência de inteiros dentro do intervalo $x\in[0,10)$:

np.arange(0,10)

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

Ou simplesmente:

np.arange(10)

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

Observe que o último elemento não está incluso.

Dica: Ele é semelhante ao range() do Python.

Podemos adicionar ao parâmentro de passo um intervalo de 0.5:

np.arange(0,10,0.5)

array([0. , 0.5, 1. , 1.5, 2. , 2.5, 3. , 3.5, 4. , 4.5, 5. , 5.5, 6. , 6.5, 7. , 7.5, 8. , 8.5, 9. , 9.5])

Função zeros:

O função zeros permite criar matriz ou vetores só de zeros. Ela tem a seguinte notação:

np.zeros(
    tamanho, # Para vetor: um número | Para matriz: Tupla com o tamanho da matriz
    dtype=[tipo] #opcional (Padrão é float)
)

Por exemplo, podemos criar um vetor de tamanho 3 só de zeros:

vetor_nulo=np.zeros(3) #Definindo um vetor nulo com 3 matrizes
display(vetor_nulo)

array([0., 0., 0.])

Ou uma matriz 5x3 de inteiros (5 linhas e 3 colunas) só com elementos nulos usando uma tupla:

matriz_nula=np.zeros((5,3),dtype=int)
display(matriz_nula)

array([[0, 0, 0],
[0, 0, 0],
[0, 0, 0],
[0, 0, 0],
[0, 0, 0]])

Ou ainda uma matriz 3D de 3x3x3:

matriz_3D_nula=np.zeros((3,3,3))
display(matriz_3D_nula)

array([[[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]],
[[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]],
[[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]]])

Função ones:

A função ones é semelhante à função zeros , só que ao invés de criar arrays nulos, cria-se arrays preenchidos com 1. Vamos refazer os exemplos anteriores:

np.ones(3)

array([1., 1., 1.])

np.ones((3,3,3))

array([[[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]],
[[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]],
[[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]]])

Função empty:

A função empty cria um array vazio, ou seja, os valores dentro da matriz não são inicializados. Sua sintaxe é parecida com as funções zeros e ones.

Para exemplificiar veja o exemplo abaixo:

d=np.empty(20)
d

array([0. , 0.5, 1. , 1.5, 2. , 2.5, 3. , 3.5, 4. , 4.5, 5. , 5.5, 6. , 6.5, 7. , 7.5, 8. , 8.5, 9. , 9.5])

Observe que a lista foi inicializada com valores “aleatórios”. Na verdade estes valores já estavam na memória, esse tipo de operação é útil quando queremos inicializar uma matriz para depois preenche-la com valores.

Matriz identidade:
Matriz identidade é uma matriz que contêm 1 na sua diagonal principal (Diagonal da direita para esquerda), e zero no restante da matriz. Abaixo a matriz $M$ é uma matriz identidade 3x3:

\[M=\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\]

A matriz identidade é sempre quadrada (O número de linhas é igual ao número de coluna).

Para criar uma matriz identidade do tamanho $n\times n$ no numpy utilizamos a função:

eye(n)

Vejamos o exemplo abaixo para a criação de uma matriz 3x3:

np.eye(3)

array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])

Considerando valores complexos:

np.eye(3,dtype=complex)

array([[1.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 1.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 1.+0.j]])

Observação: Para quem estudou algebra linear, sabe qual a importância da matriz identidade.

Função linspace:

A função linspace é semelhante ao arange só que no arange você controla o intervalo entre os valores e no linspace você controla o número de pontos. O método tem a seguinte notação:

x=linspace(
    i, #início
    f, #fim
    [no_de_pontos] # Padrão é 50 pontos (Argumento opcional)
)

onde $x\in[i,f]$.

Vejam alguns exemplos:

np.linspace(0,10) #Criamos um vetor de 0 a 10 com 50 pontos (50 pontos é o padrão)

array([ 0. , 0.20408163, 0.40816327, 0.6122449 , 0.81632653, 1.02040816, 1.2244898 , 1.42857143, 1.63265306, 1.83673469, 2.04081633, 2.24489796, 2.44897959, 2.65306122, 2.85714286, 3.06122449, 3.26530612, 3.46938776, 3.67346939, 3.87755102, 4.08163265, 4.28571429, 4.48979592, 4.69387755, 4.89795918, 5.10204082, 5.30612245, 5.51020408, 5.71428571, 5.91836735, 6.12244898, 6.32653061, 6.53061224, 6.73469388, 6.93877551, 7.14285714, 7.34693878, 7.55102041, 7.75510204, 7.95918367, 8.16326531, 8.36734694, 8.57142857, 8.7755102 , 8.97959184, 9.18367347, 9.3877551 , 9.59183673, 9.79591837, 10. ])

np.linspace(0,10,2) #Vetor de 0 a 10 com 2 pontos

array([ 0., 10.])

np.linspace(0,10,3) #Vetor de 0 a 10 com 3 pontos

array([ 0., 5., 10.])

Exemplo 3: Criação de vetores ou matrizes pseudo-aleatórias

O sub-módulo random permite trabalhar com números (pseudo)-aleatórios no numpy.

Função rand:

Dentro desse sub-módulo tem a fução rand(). Esta função permite criar um vetor de 0 a 1 seguindo uma distribuição uniforme. Para exemplificar, segue alguns exemplos.

Observação: Na distribuição uniforme todos os números tem igual probabilidade de aparecer.

np.random.rand(5)

array([0.94118875, 0.34111341, 0.80662278, 0.45170693, 0.66366523])

np.random.rand(5,3)

array([[0.60231965, 0.13915405, 0.14062354],
[0.27107605, 0.18510555, 0.21056944],
[0.10201384, 0.28359186, 0.14403438],
[0.30504466, 0.12530748, 0.51605981],
[0.99243939, 0.39609503, 0.9970822 ]])

np.random.rand(3,3,3)

array([[[0.77764142, 0.43046879, 0.53158257],
[0.64275742, 0.83375245, 0.95512209],
[0.7829738 , 0.77918175, 0.55932601]],
[[0.41110129, 0.52807456, 0.44260406],
[0.69113728, 0.31073929, 0.4410191 ],
[0.98909848, 0.42453472, 0.05985846]],
[[0.16424895, 0.41459249, 0.82175022],
[0.85997619, 0.81019046, 0.82846896],
[0.0065252 , 0.62029727, 0.15771548]]])

Neste caso basta multiplicar o vetor resultante por 10:

np.random.rand(5)*10

array([7.83576456, 1.01106823, 1.41474059, 7.40103568, 7.87425518])

Função randn

A função randn é simular à função rand, só que ao invés de usar uma distribuição uniforme, utiliza uma distribuição normal. Sua sintaxe é similar à função rand. Considerando uma distribuição normal de $X \tilde N(\mu,\sigma^2)$, onde:

Podemos encontrar a variável $Z$:

\[Z=\frac{x-\mu}{\sigma}\]

onde $Z$ é o valor retornado por randn e $x$ é um valor da amostra.

Se quisermos encontrar apenas $Z$, basta utilizar a função randn.

Veja o exemplo abaixo de uma matriz 5x3 de valores de $Z$:

np.random.randn(5,3)

array([[ 0.1472857 , -0.13911195, 0.77754573],
[ 0.74258769, 0.68650298, -0.11081065],
[-0.11407845, 0.47306611, 1.19310296],
[-0.73273615, -0.75575008, -1.23730874],
[-2.08020549, 0.5424344 , -0.96590237]])

Para encontrar as amostras $x_i$ da população devemos definir o valor da média e do desvio padrão da população, e aplicar a seguinte fórmula:

\[x=\mu+\sigma\cdot Z\]

Por exemplo, considere uma distribuição normal com média 5 e desvio padrão 1.5. Vamos criar um vetor com 5 elementos, considerando esta distribuição:

média=5
desvio_padrão=1.5
média+desvio_padrão*np.random.randn(5)

array([7.85996339, 6.19473181, 5.24679766, 6.72999723, 6.6830092 ])

Função randint:

A função randint é simular à função rand, só que retorna números inteiros. Sua sintáxe é um pouco diferente da função rand, e é mostra abaixo:

randint(i, #início
        f, #fim (Intervalo aberto)
        [no_pontos] #número de pontos (opcional)
       )

Veja com $x\in[0,100)$ e $100$ amostras:

np.random.randint(0,100,10)

array([ 3, 90, 63, 58, 27, 61, 64, 78, 11, 10])

Usando o rand para recriar um “randint”:

Podemos recriar o método randint com a função rand. Basta utilizar o método de arrays round:

(100*np.random.rand(10)).round(0)

array([93., 39., 94., 33., 8., 18., 11., 44., 60., 51.])

Ou ainda:

np.round((100*np.random.rand(10)),0)

array([76., 69., 3., 66., 75., 1., 45., 55., 19., 94.])

A diferença desse método para o randint é que a resultante é um array de float e o intervalo final é fechado.

Exemplo 4: Métodos e atributos de arrays

Método reshape:

O método reshape permite mudar o formato do array. Desta forma, podemos tranformar vetores em matrizes ou em matrizes 3, e vice-versa. Seus argumentos são similares às funções zeros e ones.

Para exemplificar, veja o exemplo abaixo:

arr=np.linspace(10,270,27) #Array com 27 elementos
display(arr)

array([ 10., 20., 30., 40., 50., 60., 70., 80., 90., 100., 110., 120., 130., 140., 150., 160., 170., 180., 190., 200., 210., 220., 230., 240., 250., 260., 270.])

arr=arr.reshape((3,9))
arr

array([[ 10., 20., 30., 40., 50., 60., 70., 80., 90.], [100., 110., 120., 130., 140., 150., 160., 170., 180.], [190., 200., 210., 220., 230., 240., 250., 260., 270.]])

arr=arr.reshape((3,3,3))
arr

array([[[ 10., 20., 30.],
[ 40., 50., 60.],
[ 70., 80., 90.]],
[[100., 110., 120.],
[130., 140., 150.],
[160., 170., 180.]],
[[190., 200., 210.],
[220., 230., 240.],
[250., 260., 270.]]])

Método astype:

Converte array de um tipo em outro tipo. Por exemplo, podemos transformar o vetor arr em uma matriz 3x3x3 de complex:

arr.reshape(3,3,3).astype(complex)

array([[[ 10.+0.j, 20.+0.j, 30.+0.j],
[ 40.+0.j, 50.+0.j, 60.+0.j],
[ 70.+0.j, 80.+0.j, 90.+0.j]],
[[100.+0.j, 110.+0.j, 120.+0.j],
[130.+0.j, 140.+0.j, 150.+0.j],
[160.+0.j, 170.+0.j, 180.+0.j]],
[[190.+0.j, 200.+0.j, 210.+0.j],
[220.+0.j, 230.+0.j, 240.+0.j],
[250.+0.j, 260.+0.j, 270.+0.j]]])

Atributo shape:

Enquanto o método executa uma ação de um determinado objeto, o atributo é uma característica de um objeto.

Um dos atributos dos objetos array é o shape. Ele indica o formato do array. Veja o exemplo para a matriz 3D arr:

arr.shape

(3, 3, 3)

Atributo size:

O atributo size indica a quantidade de elementos do array. Veja o exemplo para arr:

arr.size

27

Métodos max, min, mean e std:

Estes métodos retornam o valor máximo, valor mínimo, valor médio e desvio padrão, respectivamente.

Veja os exemplos para a matriz 3D arr:

arr.max() #Máximo de arr

270.0

arr.min() #Mínimo de arr

10.0

arr.mean() #Média do vetor

140.0

arr.std() #Desvio padrão do vetor

77.88880963698615

Métodos argmax e argmin:

Retornam o índice na qual o maior ou o menor elemento se encontram:

i=arr.argmax()
i

26

Se quisermos saber o maior elemento a partir do argmax():

print('O valor do índice de maior elemento:',i)
print('O maior elemento:',arr.reshape(arr.size)[i])

O valor do índice de maior elemento: 26
O maior elemento: 270.0

O argmin é similar:

i=arr.argmin()
print('O valor do índice de menor elemento:',i)
print('O menor elemento:',arr.reshape(arr.size)[i])

O valor do índice de menor elemento: 0
O menor elemento: 10.0

Exemplo 5: Indexação e fatiamento de arrays

A indexação e fatiamento de arrays é similar às indexação e fatiamento nas variáveis compostas, como listas, tuplas e strings. Para exemplificar vamos utilizar o array abaixo e aplicar algumas operações.

# Criando um array de inteiros com o intervalo 0 a 145 de 5 em 5
arr = np.arange(0,150,5,dtype=int)
arr

array([ 0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105, 110, 115, 120, 125, 130, 135, 140, 145])

arr[-1]

145

arr[2:]=150
arr

array([ 0, 5, 150, 150, 150, 150, 150, 150, 150, 150, 150, 150, 150, 150, 150, 150, 150, 150, 150, 150, 150, 150, 150, 150, 150, 150, 150, 150, 150, 150])

Trabalhando com matrizes:

arr = np.arange(0,150,5,dtype=int).reshape(6,5) #Transformando o arr em uma matriz 6x5
arr

array([[ 0, 5, 10, 15, 20],
[ 25, 30, 35, 40, 45],
[ 50, 55, 60, 65, 70],
[ 75, 80, 85, 90, 95],
[100, 105, 110, 115, 120],
[125, 130, 135, 140, 145]])

arr[-1,:]

array([125, 130, 135, 140, 145])

Ou ainda, usando a notação de lista:

arr[-1][:]

array([125, 130, 135, 140, 145])

Ou ainda:

arr[-1]

array([125, 130, 135, 140, 145])

arr[:,2:]

array([[ 10, 15, 20],
[ 35, 40, 45],
[ 60, 65, 70],
[ 85, 90, 95],
[110, 115, 120],
[135, 140, 145]])

Método copy:

Digamos que queremos criar um subarray de arr e atribuir o valor 30 para todos os elementos desse subarray:

arr = np.arange(0,150,5,dtype=int).reshape(6,5) #Transformando o arr em uma matriz 6x5
arr2=arr[3:][:]
arr2

array([[ 75, 80, 85, 90, 95],
[100, 105, 110, 115, 120],
[125, 130, 135, 140, 145]])

arr2[:]=100
display(arr2)

array([[100, 100, 100, 100, 100],
[100, 100, 100, 100, 100],
[100, 100, 100, 100, 100]])

display(arr)

array([[ 0, 5, 10, 15, 20],
[ 25, 30, 35, 40, 45],
[ 50, 55, 60, 65, 70],
[100, 100, 100, 100, 100],
[100, 100, 100, 100, 100],
[100, 100, 100, 100, 100]])

Observe que o valor de arr foi alterado também. Para corrigir vamos utilizar o método copy:

arr = np.arange(0,150,5,dtype=int).reshape(6,5) #Transformando o arr em uma matriz 6x5
arr2=arr[3:][:].copy()
arr2[:]=100
display(arr2)

array([[100, 100, 100, 100, 100],
[100, 100, 100, 100, 100],
[100, 100, 100, 100, 100]])

display(arr)

array([[ 0, 5, 10, 15, 20],
[ 25, 30, 35, 40, 45],
[ 50, 55, 60, 65, 70],
[ 75, 80, 85, 90, 95],
[100, 105, 110, 115, 120],
[125, 130, 135, 140, 145]])

Neste caso o método copy criou uma cópia do subarray de arr em arr2, ao invés de passar a referência.

Seleção ou fatiamento por condicionais:

Se executarmos o código abaixo, será retornado um array de booleanos:

bol=arr > 50

array([[False, False, False, False, False],
[False, False, False, False, False],
[False, True, True, True, True],
[ True, True, True, True, True],
[ True, True, True, True, True],
[ True, True, True, True, True]])

Podemos usar este array para fazer fatiamento de arrays:

arr[bol]

array([ 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105, 110, 115, 120, 125, 130, 135, 140, 145])

Ou ainda modificar valores de um array:

arr[arr>=50]=-1
arr

array([[ 0, 5, 10, 15, 20],
[25, 30, 35, 40, 45],
[-1, -1, -1, -1, -1],
[-1, -1, -1, -1, -1],
[-1, -1, -1, -1, -1],
[-1, -1, -1, -1, -1]])

Exemplo 6: Operação com arrays

Diferente das listas, os arrays nos permite operar de forma muito mais simples.

Primeiro vamos criar um array:

arr = np.arange(0,50,5)
display(arr)

array([ 0, 5, 10, 15, 20, 25, 30, 35, 40, 45])

E fazer algumas operações

Somando arrays:

# Somando arrays
arr + arr

array([ 0, 10, 20, 30, 40, 50, 60, 70, 80, 90])

Multiplicando arrays:

#Multiplicação
arr2=arr*arr
arr2

array([ 0, 25, 100, 225, 400, 625, 900, 1225, 1600, 2025])

Subtraindo arrays:

#Subtraindo arrays
arr2-arr

array([ 0, 20, 90, 210, 380, 600, 870, 1190, 1560, 1980])

Divisão de arrays:

arr/arr

array([nan, 1., 1., 1., 1., 1., 1., 1., 1., 1.])

Observe que o valor inicial foi nan, porque 0/0 é indeterminado. Vamos tentar a divisão por zero:

1/arr

array([ inf, 0.2 , 0.1 , 0.06666667, 0.05 , 0.04 , 0.03333333, 0.02857143, 0.025 , 0.02222222])

Observe que 1/0 é infinito.

Exponenciação:

arr**2

array([ 0, 25, 100, 225, 400, 625, 900, 1225, 1600, 2025])

Somando com uma constante:

arr+5

array([ 5, 10, 15, 20, 25, 30, 35, 40, 45, 50])

Raiz quadrada:

np.sqrt(arr)

array([0. , 2.23606798, 3.16227766, 3.87298335, 4.47213595, 5. , 5.47722558, 5.91607978, 6.32455532, 6.70820393])

Funções trigonométricas:

np.cos(arr)

array([ 1. , 0.28366219, -0.83907153, -0.75968791, 0.40808206, 0.99120281, 0.15425145, -0.90369221, -0.66693806, 0.52532199])

np.sin(arr)

array([ 0. , -0.95892427, -0.54402111, 0.65028784, 0.91294525, -0.13235175, -0.98803162, -0.42818267, 0.74511316, 0.85090352])

np.tan(arr)

array([ 0. , -3.38051501, 0.64836083, -0.8559934 , 2.23716094, -0.13352641, -6.4053312 , 0.47381472, -1.11721493, 1.61977519])

Funções inversas trigonométricas:

cos=np.linspace(0,1,3)
print('Cosseno:',cos)
print('Arco cosseno:',np.arccos(cos)*180/np.pi)

Cosseno: [0. 0.5 1. ]
Arco cosseno: [90. 60. 0.]

Média, mínimo, máxima, soma e desvio padrão:

Uma outra forma de encontrar os valores mínimo, máximo, soma e média e desvio padrão é através das funções correspondentes:

np.mean(arr) #Média

22.5

np.max(arr) #Máximo

45

np.min(arr) #Mínimo

0

np.sum(arr) #Soma

225

np.std(arr) #Desvio padrão

14.361406616345072

Outras funções:

Existem muitas outras funções que estão disponíveis na documentação:

https://numpy.org/doc/stable/reference/ufuncs.html

Tarefa 1: Matriz complexa

Considere uma matriz complexa: \(A= \begin{bmatrix} 6 + 2j & 12 + 4j & 18 + 6j & 24 + 8j & 30 + 10j \\ 36 + 12j & 42 + 14j & 48 + 16j & 54 + 18j & 60 + 20j \\ 66 + 22j & 72 + 24j & 78 + 26j & 84 + 28j & 90 + 30j \\ 96 + 32j & 102 + 34j & 108 + 36j & 114 + 38j & 120 + 40j \\ 126 + 42j & 132 + 44j & 138 + 46j & 144 + 48j & 150 + 50j \end{bmatrix}\)

  1. Crie essa matriz utilizando a função arange ou linspace e o método reshape
  2. Calcule o conjugado dessa matriz (Veja a documentação)
  3. Selecione a segunda coluna desta matriz

Solução:

from IPython.display import Markdown as md

A=(np.arange(6,151,6)+1j*np.arange(2,51,2)).reshape(5,5)
print('1.')
display(A)
print('2.')
display(np.conjugate(A))
print('3.')
display(A[:,1])

Exemplo 7: Matrizes

As matrizes tem algumas particularidades em relação aos escalares. Desta forma, precisamos de um maior cuidado em relação à operação esses elementos.

Matriz transposta:

Para calcular a matriz transposta podemos utilizar o atributo T. da matriz.

Primeiramente vamos criar uma matriz:

A=np.arange(6).reshape(3,2)
display(A)

array([[0, 1],
[2, 3],
[4, 5]])

Depois podemos calcular a transposta como é mostrado abaixo:

A.T

array([[0, 2, 4], [1, 3, 5]])

Ou ainda, a função ou o método transpose:

# Função transpose
np.transpose(A)

array([[0, 2, 4], [1, 3, 5]])

# Método transpose
A.transpose()

array([[0, 2, 4], [1, 3, 5]])

Multiplicação de matrizes:

A multiplicação de matrizes é diferente da multiplicação de escalar. Como o numpy sempre faz as operações termo a termo, para fazer a multiplicação de matrizes devemos utilizar uma função específica para isso, que no caso é a função dot().

Vamos fazer a seguinte operação $B=A\cdot A^T$:

B=np.dot(A,A.T)
display(B)

array([[ 1, 3, 5], [ 3, 13, 23], [ 5, 23, 41]])

Multiplicação de matrizes (termo a termo):

Para fazer a multiplicação de matrizes termo a termo, basta multiplicar normalmente:

A*A

array([[ 0, 1], [ 4, 9], [16, 25]])

Diagonal principal:

Para retornar a diagonal principal de uma matriz basta usar a função diagonal:

C=np.diagonal(B)
C

array([ 1, 13, 41])

Matriz diagonal:

Podemos usar a função diagflat para criar uma matriz diagonal (Matriz com elementos não nulos na diagonal principal e elementos nulos fora da diagonal principal):

np.diagflat(C)

array([[ 1, 0, 0],
[ 0, 13, 0],
[ 0, 0, 41]])

Observação: Podemos usar a função diag() para encontrar a diagonal principal de uma matriz e para criar matrizes diagonal. Ela é uma função de compatibilidade com MATLAB.

np.diag(B)

array([ 1, 13, 41])

np.diag(np.diag(B))

array([[ 1, 0, 0],
[ 0, 13, 0],
[ 0, 0, 41]])

Diagonal secundária:

Para obter a diagonal secundária devemos “girar” da esquerda para a direta a matriz usando a função fliplr(). Primeiramente vamos repetir a matriz B:

B

array([[ 1, 3, 5],
[ 3, 13, 23],
[ 5, 23, 41]])

Depois vamos “girar” a matriz B utilizando fliplr:

np.fliplr(B)

array([[ 5, 3, 1],
[23, 13, 3],
[41, 23, 5]])

Para calcular a sua diagonal secundária, logo em seguida:

np.diagonal(np.fliplr(B))

array([ 5, 13, 5])

Matriz inversa:

Para determinar a matriz inversa podemos utilizar o submódulo de algebra linear, o linalg. Dentro desse sub-módulo existe a função ìnv que calcula a inversa do vetor.

Por exemplo, considere uma matriz: \(D= \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\)

D=np.array([[1,2],[3,4]])

E queremos calcular a matriz inversa de $D$:

np.linalg.inv(D)

array([[-2. , 1. ],
[ 1.5, -0.5]])

Determinante:

Para calcular o determinante podemos recorer a função det do submódulo linalg. Podemos calcular o determinante de $D$:

np.linalg.det(D)

-2.0000000000000004

Outras operações com matrizes:

O Numpy têm várias funções prontas para o cálculo de problemas de algebra linear. Todas as funções pode ser encontrado na documentação:

https://numpy.org/doc/stable/reference/routines.linalg.html

Tarefa 2: Sistema linear

Considere um sistema linear com as seguintes equações:

\[\begin{cases} 2x+y+3z=4\\ x-y+5z=3\\ 3x+y-2z=1 \end{cases}\]

Para resolver este sistema linear podemos escrevê-lo na forma matricial:

\[A\cdot W=B\]

onde:

\[A=\begin{bmatrix} 2 & 1 & 3\\ 1 & -1 & 5\\ 3 & 1 & -2 \end{bmatrix}\] \[W=\begin{bmatrix} x \\ y \\ z \end{bmatrix}\] \[B=\begin{bmatrix} 4 \\ 3 \\ 1 \end{bmatrix}\]

A solução deste sistema linear é: \(W=A^{-1}\cdot B\)

Responda utilizando o numpy:

  1. Calcule o determinante de A
  2. Calcule a inversa de A
  3. Resolva este sistema linear utizando a definição acima.
  4. Resolva este sistema linear utilizando a função solve do submódulos

Solução:

#Definindo as matrizes
A=np.array([[2,1,3],[1,-1,5],[3,1,-2]])
display(A)
B=np.array([4,3,1]).reshape(3,1)
display(B)
  1. Determinante
DetA=np.linalg.det(A)
display(DetA)
  1. Inversa
InvA=np.linalg.inv(A)
display(InvA)
  1. Resolução do sistema linear
from IPython.display import Markdown as md

W=np.dot(InvA,B)
md(fr"""
A solução da equação é:
\begin
    x={float(W[0])}\\
    y={float(W[1])}\\
    z={float(W[2])}
\end
""")
  1. Resolva este sistema linear utilizando a função solve do submódulos
W=np.linalg.solve(A,B)
md(fr"""
A solução da equação é:
\begin
    x={float(W[0])}\\
    y={float(W[1])}\\
    z={float(W[2])}
\end
""")

Exemplo 8: Concatenação de arrays

A concatenação de arrays pode ser feita através da função concatenate que tem a seguinte notação:

concatenate(
    tupla_com_os_arrays,
    [axis] #Eixo opcional
    )

Vamos criar dois arrays a e b:

a = np.arange(6).reshape(3,2)
b = (np.ones(6)).reshape(3,2)

Eixo 0 concatena nas colunas:

np.concatenate((a,b),axis=0) # Eixo 0 concatena nas colunas

array([[0., 1.],
[2., 3.],
[4., 5.],
[1., 1.],
[1., 1.],
[1., 1.]])

Eixo 1 concatena nas linhas:

np.concatenate((a,b),axis=1) #Eixo 1 concatena nas linhas

array([[0., 1., 1., 1.], [2., 3., 1., 1.], [4., 5., 1., 1.]])

Exemplo 9: Perfomance do Numpy

Vimos que na teoria o numpy é muito mais eficiente que trabalhar com lista. Vamos comparar na prática, comparando o método range() para criar listas e o método arange() para criar arrays.

Memória do numpy vs list:

#importando o módulo system para medir o tamanho da lista
import sys

Lista=list(range(1000)) #Declarando uma tupla de 0 a 999
Numpy_Array=np.arange(1000) #Declarando um numpy array de 0 a 999
print('Tamanho de cada elemento da lista em bytes:',sys.getsizeof(Lista))
print('Tamanho total da lista em bytes:',sys.getsizeof(Lista)*len(Lista))
print('Tamanho de cada elemento do numpy array em bytes:',Numpy_Array.itemsize)
print('Tamanho total do numpy array em bytes:',Numpy_Array.itemsize*Numpy_Array.size)

Tamanho de cada elemento da lista em bytes: 8056
Tamanho total da lista em bytes: 8056000
Tamanho de cada elemento do numpy array em bytes: 8
Tamanho total do numpy array em bytes: 8000

Velocidade de execução das operações:

No nosso segundo teste de desempenho vamos comparar a operação de $x^2$, onde $x$ pertence a um vetor de 1 milhão de elementos. Para medir o tempo de execução iremos utilizar o módulo time.

import time #importando o módulo time

Criando a lista e o array:

lista = list(range(1000000))  #Criando uma lista de 1 milhão de elementos
array = np.arange(1000000) #Criando um array de 1 milhão de elementos
# Fazendo calculando o valor quadrado da lista e do array

arrayQuadrado = array**2

Medindo o tempo da operação em uma lista:

for i in range(10):
    Tempo_inicial = time.time()  #Iniciando o contador
    listaQuadrado = [i**2 for i in lista]
    Tempo_gasto=time.time()-Tempo_inicial
    print(i,'- O tempo gasto foi:',Tempo_gasto*1000,'ms')

0 - O tempo gasto foi: 177.23417282104492 ms
1 - O tempo gasto foi: 181.779146194458 ms
2 - O tempo gasto foi: 193.6969757080078 ms
3 - O tempo gasto foi: 186.5365505218506 ms
4 - O tempo gasto foi: 177.30140686035156 ms
5 - O tempo gasto foi: 179.00490760803223 ms
6 - O tempo gasto foi: 185.7607364654541 ms
7 - O tempo gasto foi: 180.2222728729248 ms
8 - O tempo gasto foi: 185.9571933746338 ms
9 - O tempo gasto foi: 177.34956741333008 ms

Medindo o tempo da operação em um numpy array:

for i in range(10):
    Tempo_inicial = time.time()  #Iniciando o contador
    listaQuadrado = array**2
    Tempo_gasto=time.time()-Tempo_inicial
    print(i,'- O tempo gasto foi:',Tempo_gasto*1000,'ms')

0 - O tempo gasto foi: 7.731437683105469 ms
1 - O tempo gasto foi: 1.1243820190429688 ms
2 - O tempo gasto foi: 0.8718967437744141 ms
3 - O tempo gasto foi: 0.7486343383789062 ms
4 - O tempo gasto foi: 0.7238388061523438 ms
5 - O tempo gasto foi: 0.7958412170410156 ms
6 - O tempo gasto foi: 0.7092952728271484 ms
7 - O tempo gasto foi: 0.7219314575195312 ms
8 - O tempo gasto foi: 0.6957054138183594 ms
9 - O tempo gasto foi: 0.7140636444091797 ms

Atividade 2: Matplotlib

Matplolib é uma biblioteca de criação de gráficos mais popular do Python. De uma forma geral, as outras bibliotecas são derivadas da biblioteca Numpy. Podemos dizer que ela biblioteca mãe de todas as outras funções e/ou bibliotecas de visualização dados. Além disso Matplotlib é muito poderoso, pois ela dá controle sob todos os aspectos da figura e foi projetada para ser semelhante ao MATLAB.

A documentação do Matplotlib pode ser acessada abaixo:

https://matplotlib.org/

Dentro da documentação é possível ver uma aba de exemplos (Gallery):

https://matplotlib.org/gallery/index.html

Nesta página é possível ver tudo que é possível fazer com essa biblioteca. Com uma série de gráficos e funcionalidades diferentes.

Exemplo 1: Primeiro gráfico

No matplotlib quase sempre utilizamos o sub-módulo pyplot, desta forma podemos importar essa subclasse como mostrado abaixo, geralmente apelidamos este sub-módulo como plt:

import matplotlib.pyplot as plt

A principal função de plotagem é a função plot, ela tem a seguinte notação:

plot(x, #Array com os valores do eixo x
     y #Array com os valores do eixo y

É importante frisar que esta notação do plot é semelhante à plotagem paramétrica.

Caso queiramos plotar apenas a informação do y podemos usar a seguinte notação:

plot(y #Array com os valores do eixo y
)

Nesse caso o espaçamento entre os pontos de y será 1.

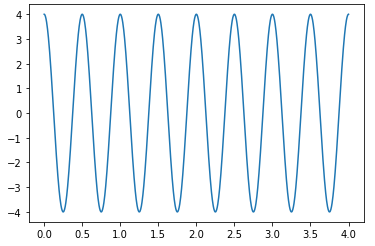
Para exemplificar o nosso primeiro gráfico vamos plotar uma onda:

\[f(t)=4\cos(4\pi\cdot t)\] 
t=np.linspace(0,4,1000) #Criando um vetor de tempo com 1000 pontos
plt.plot(t, #Primeiro argumento é o x
         4*np.cos(4*np.pi*t), #Segundo argumento é o y
        );

Primeiro gráfico

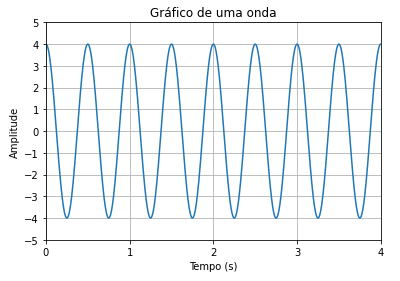
Podemos customizar o nosso gráfico através das seguintes funções:

plt.plot(t,4*np.cos(4*np.pi*t)); #Ploto o gráfico de cor vermelha
plt.xlabel('Tempo (s)'); #Adiciono o título do eixo x como 'Tempo (s)'
plt.ylabel('Amplitude'); #Adiciono o título do eixo y como 'Amplitude'
plt.grid(True); #Coloco uma grid no gráfico
plt.title('Gráfico de uma onda'); #Adiciono um título ao gráfico
plt.xlim(0,4); #Digo que os limites de tempo (Eixo x) do gráfico é de [0,4]
plt.ylim(-5,5); #Digo que os limites de tempo (Eixo y) do gráfico é de [-5,5]
plt.xticks(np.arange(5)); #Digo onde estarão os indicadores do eixo x
plt.yticks(np.arange(-5,6,1)); #Digo onde estarão os indicadores do eixo y

Primeiro gráfico customizado

Exemplo 2: Customização e plotagem de múltiplos gráficos

Neste segundo exemplo vamos aprender a plotar mais de um gráfico na mesma figura e customizar a linha de cada gráfico. Para isso vamos utilizar as seguintes equações:

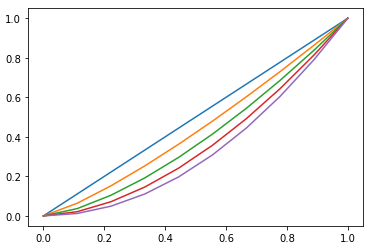
\[\begin{cases} y_1(t)=t\\ y_2(t)=t^{1.25}\\ y_3(t)=t^{1.5}\\ y_4(t)=t^{1.75}\\ y_5(t)=t^{2} \end{cases}\]

Plotando múltiplos gráficos:

Para plotar mais de um gráfico na mesma figura é muito simples, basta escrever outro gráfico depois do outro.

Primeiramente vamos criar o vetor do eixo x:

t=np.linspace(0,1,10) #Criando um vetor de 0 a 1 com 10 pontos

Depois plotamos os gráficos:

# Plot
plt.plot(t,t);
plt.plot(t,t**1.25);
plt.plot(t,t**1.5);
plt.plot(t,t**1.75);
plt.plot(t,t**2);

Multiplos gráficos

Observe que o próprio matplotlib definiu cores diferentes para cada gráfico. Assim fica fácil identificá-los. Entretanto podemos customizá-los.

Customização dos gráficos:

O terceiro parâmetro da função plot é o parâmetro de abreviação de estilo da linha do gráfico. Nele podemos alterar os seguintes aspectos:

O parâmetro deve ser escrito na forma de string seguindo a seguinte ordem cor+estilo+marcação.

Abaixo segue as abreviações de algumas cores disponíveis:

Abreviação Cor Nome completo
r Vermelho red
g Verde green
b Azul blue
k Preto black
y Amarelo yellow
m Magenta magenta
c Ciano cyan
w Branco ẁhite

Além dessas, existem outras cores nomeadas que podem ser encontradas na documentação:

https://matplotlib.org/3.1.0/gallery/color/named_colors.html

O estilo da linha também tem abreviações, que são apresentados abaixo:

Abreviação Estilo de linha Nome completo
- Linha sólida solid
-- Trecejado dashed
-. Tracejado com ponto dashdot
: Ponteado dotted

Por fim, como a lista de marcadores são muito grande, é interessante olhar a documentação para mais detalhes.

https://matplotlib.org/api/markers_api.html

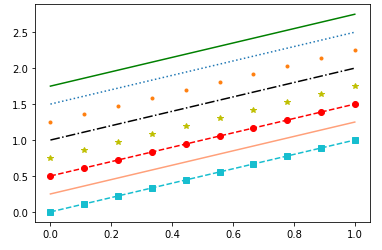
No exemplo abaixo temos alguns estilos possíveis:

t=np.linspace(0,1,10)

# Cor ou estilo ou marcador (Os parâmetros ausentes terão os valores padrão)

plt.plot(t,t+1.75,'g'); #Apenas cor
plt.plot(t,t+1.5,':'); #Apenas estilo
plt.plot(t,t+1.25,'.'); #Apenas marcador

#Cor + estilo:
plt.plot(t,t+1,'k-.'); #Cor preta com tracejados e pontos

#Cor + marcador
plt.plot(t,t+0.75,'y*'); #Cor magenta com marcador de *

#Cor + estilo + marcador
plt.plot(t,t+0.5,'r--o'); #Cor vermelha com tracejados e marcador de bola

#Cor sem abreviação
plt.plot(t,t+0.25,'lightsalmon'); #Colocando uma cor diferente das abreviadas

#Customizando cada parâmetro seperadamente utilizando os nomes dos parâmetros correspondentes
plt.plot(t,t,color='tab:cyan',linestyle='--',marker='s');

Terceiro gráfico

Tarefa 3: Customização avançada

Crie dois gráficos sobrepostos de uma equação de terceiro grau: \(y(t)=x^3\)

com $t\in[-2,2]$ e 10 pontos.

Utilizando os seguintes parâmetros de linha para o primeiro gráfico:

E os seguintes parâmetros para o segundo gráfico:

Solução:

t=np.linspace(-2,2,10)

plt.plot(t,t**2,color='k',linestyle='--',marker='+')
plt.plot(t,t**2,color='#e69900',linewidth=20,alpha=0.5);

Exemplo 3: Sub-gráficos (Subplot)

Dentro de uma mesma figura é possível criar mais de um “plot”, para isso vamos recorrer a função subplot. A função subplot tem a seguinte notação:

subplot(
    nrows, #Número de linhas que será dividida a figura
    ncols, #Número de coluna que será dividida a figura
    index #Posição da do subplot
)

Para ficar mais claro vamos tentar plotar o exemplo anterior em gráficos diferentes.

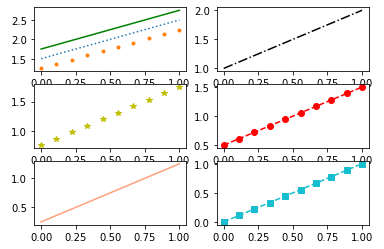
t=np.linspace(0,1,10)

#Subplot 1 - Cor ou estilo ou marcador
plt.subplot(
    3, #Irei dividir a minha figura em 3 linhas
    2, # 2 colunas
    1 # Esse será o primeiro subplot
) 

plt.plot(t,t+1.75,'g'); #Apenas cor
plt.plot(t,t+1.5,':'); #Apenas estilo
plt.plot(t,t+1.25,'.'); #Apenas marcador

#Subplot 2 - Cor + estilo
plt.subplot(3,2,2) #Nomear os parâmetros é opcional
plt.plot(t,t+1,'k-.');

#Subplot 3 - Cor + marcador
plt.subplot(3,2,3)
plt.plot(t,t+0.75,'y*');

#Subplot 4 - Cor + estilo + marcador
plt.subplot(3,2,4)
plt.plot(t,t+0.5,'r--o'); #Cor vermelha com tracejados e marcador de bola

#Subplot 5 - Cor + abreviação
plt.subplot(3,2,5)
plt.plot(t,t+0.25,'lightsalmon'); #Colocando uma cor diferente das abreviadas

#Subplot 6 - Configurando os parâmetros separadamente
plt.subplot(3,2,6)
plt.plot(t,t,color='tab:cyan',linestyle='--',marker='s');
# O parâmetro color suportar cores hexadecimais

Subfiguras

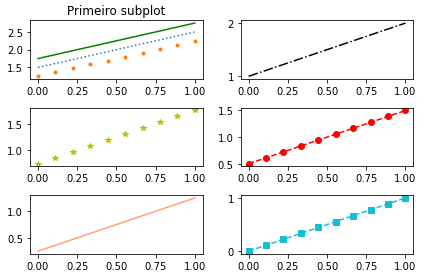
Em cada subplot pode ser feito customizações de forma isolada, por exemplo, podemos adicionar um título no primeiro subplot e utilizar a função tight_layout() para cuidar das sobreposições:

t=np.linspace(0,1,10)

#Subplot 1 - Cor ou estilo ou marcador
plt.subplot(
    3, #Irei dividir a minha figura em 3 linhas
    2, # 2 colunas
    1 # Esse será o primeiro subplot
) 

plt.plot(t,t+1.75,'g'); #Apenas cor
plt.plot(t,t+1.5,':'); #Apenas estilo
plt.plot(t,t+1.25,'.'); #Apenas marcador
plt.title('Primeiro subplot')

#Subplot 2 - Cor + estilo
plt.subplot(3,2,2) #Este será o segundo subplot
plt.plot(t,t+1,'k-.');

#Subplot 3 - Cor + marcador
plt.subplot(3,2,3)
plt.plot(t,t+0.75,'y*');

#Subplot 4 - Cor + estilo + marcador
plt.subplot(3,2,4)
plt.plot(t,t+0.5,'r--o'); #Cor vermelha com tracejados e marcador de bola

#Subplot 5 - Cor + abreviação
plt.subplot(3,2,5)
plt.plot(t,t+0.25,'lightsalmon'); #Colocando uma cor diferente das abreviadas

#Subplot 6 - Configurando os parâmetros separadamente
plt.subplot(3,2,6)
plt.plot(t,t,color='tab:cyan',linestyle='--',marker='s');

#Usando o método tight_layout para cuidar das sobreposições
plt.tight_layout()

Melhorando o grafico

Exemplo 4: Abordagem orientada a objeto

A forma que a vimos até o momento é a forma mais rápida de criação de gráficos, nela utilizamos funções para a criação e customização dos gráficos, porém ela não dá controle completo sobre todos os elementos das imagens. Uma forma utilizada na criação de gráfico é através da abordagem orientada a objeto, que será exemplificada nesse exemplo.

Figura:

Figura é nada mais nada menos que “uma caixa” onde os gráficos e/ou desenho são plotados em figuras.

Para criar uma figura vazia basta utilizamos a função figure(). Nesta função temos interesse em dois parâmetros:

figure(figsize, #Controla o tamanho da figura figsize=(largura,altura)
       dpi #"Qualidade" da figura
      )

Então vamos criar a figura:

fig = plt.figure(figsize=(6,6),dpi=100); #Criação de uma figura vazia de tamanho 6 x 6 com 100 dpi

<Figure size 600x600 with 0 Axes>

Observe que a figura vazia não tem nenhum eixo.

Eixo:

Eixo é nada mais nada menos que um retângulo no qual fica inserido o gráfico.

Podemos adicionar este eixo através do método add_axes. O método add_axes recebe um retângulo com 4 argumentos:

fig.add_axes([esquerda,direita,largura,altura])

onde:

fig = plt.figure(figsize=(6,6),dpi=100); #Criação do objeto fig da classe Figure
ax1 = fig.add_axes([
    0.05, #5% de margem esquerda
    0.05, #5% de margem direita
    0.9, #90% de largura
    0.8  #80% de altura
])

Figura com um eixo vazia

Criando o gráfico:

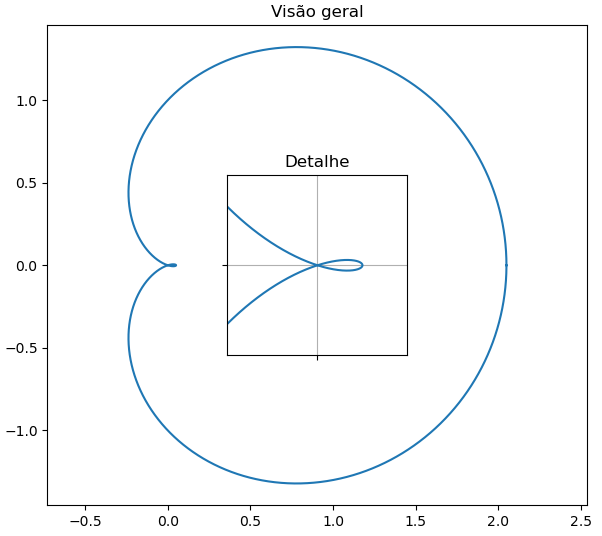
Neste exemplo vamos criar um limaçon cuja a fórmula é apresentada abaixo:

\[h(\theta)=\begin{cases} x(\theta)=r(\theta)\cdot \cos(\theta)\\ y(\theta)=r(\theta)\cdot \sin(\theta) \end{cases}\]

onde:

\[r(\theta)=a+b\cos(\theta)\]

No nosso exemplo iremos utilizar $a=1$ e $b=1.05$.

theta=np.linspace(0,2*np.pi,10000) #Criando o vetor theta

#Definindo o valor de p
r=1+1.05*np.cos(theta)

#Definindo os valores de x e y

x=r*np.cos(theta)
y=r*np.sin(theta)

fig = plt.figure(figsize=(6,6),dpi=100); #Criando a figura
ax_maior = fig.add_axes([0.05,0.05,0.9,0.8]); #Criando o primeiro eixo

#Plotando o gráfico
ax_maior.plot(x,y);

#Customização do eixo
ax_maior.axis('equal') #Selecionando o aspecto do eixo para igual
ax_maior.set_title('Visão geral'); #Adiciona título ao gráfico

#Adicionando o segundo eixo (Detalhe)
ax_menor = fig.add_axes([0.35,0.3,0.3,0.3]); 
ax_menor.plot(x,y); 

#Geralmente os métodos de axis são parecidos com as funções apresentadas anteriormente
ax_menor.set_yticks([0]); #Modificando 
ax_menor.set_xticks([0]);
ax_menor.set_xlim(-0.1,0.1);
ax_menor.set_ylim(-0.1,0.1);
ax_menor.set_title('Detalhe');
ax_menor.grid(True);

#Removendo as labels dos ticks de x e y
ax_menor.set_xticklabels(''); 
ax_menor.set_yticklabels('');

Exemplo de um limaçon

Tarefa 4: Abordagem orientada à objeto

Refaça o Exemplo 1 utilizando a abordagem orientada à objeto. Considere:

Solução:

#Defino o vetor de tempo
t=np.linspace(0,10,1000);

#Crio a figura
fig=plt.figure(figsize=[6,3],dpi=100);

#Crio o eixo
ax=fig.add_axes([0.1,0.1,0.9,0.9]);

ax.plot(t,4*np.cos(4*np.pi*t),'r--');
ax.set_xlabel('Tempo (s)');
ax.set_ylabel('Amplitude');
ax.grid(True);
ax.set_title('Gráfico de uma onda');
ax.set_xlim(0,4);
ax.set_ylim(-5,5);
ax.set_xticks(np.arange(5));
ax.set_yticks(np.arange(-5,6,1));

Exemplo 5: Subplots

No exemplo anterior aprendemos a criar um gráfico através da abordagem orientada a objeto. Para isso, precisamos criar uma figura e um eixo. A função subplots cria a figura e cria o eixo, facilitando a criação da imagem. Alguns argumentos do subplots é apresentado abaixo:

subplots(
    figsize, # Tamanho da figura
    dpi, # 'dots per inches' da figura
    nrows, #Número de linhas que minha figura será dividida
    ncols #Número de colunas que minha figura será dividida
)

Para exemplificar a função subplots iremos fazer um exemplo bem simples:

fig, ax = plt.subplots(figsize=(6,6),dpi=100) #Invocando a função subplots que retorna a figura e o eixo

x = np.linspace(-2,2,1000);

ax.plot(x,x**3,'r-');
ax.plot(x,x**2,'k--')
ax.set_xlabel('Eixo x');
ax.set_ylabel('Eixo y');
ax.set_ylim(-4,4);
ax.grid(True);

Exemplo do subplots

Exemplo 6: Adicionando legenda

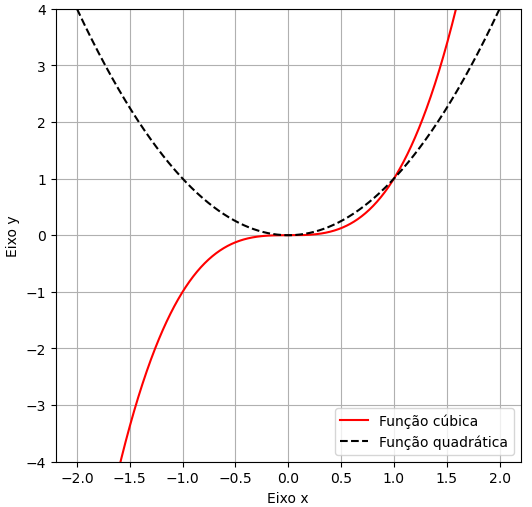
Para adicionar legenda podemos utilizar o método legend, para isso devemos adicionar ao método plot o argumento label:

fig, ax = plt.subplots(figsize=(6,6),dpi=100)

x = np.linspace(-2,2,1000);

#Adicionando as labels (Nomes) dos gráficos
ax.plot(x,x**3,'r-',label='Função cúbica');
ax.plot(x,x**2,'k--',label='Função quadrática')

ax.set_xlabel('Eixo x');
ax.set_ylabel('Eixo y');
ax.set_ylim(-4,4);
ax.grid(True);

ax.legend(); #Imprimindo a legenda

Adicionando suporte à legenda

Observação: Existe a função plt.legend() que permite a criação de legendas utilizando a abordagem funcional.

Tarefa 5: Argumento loc

Utilize o argumento loc no método legend para mudar a posição da legenda para o canto inferior esquerdo.

Solução:

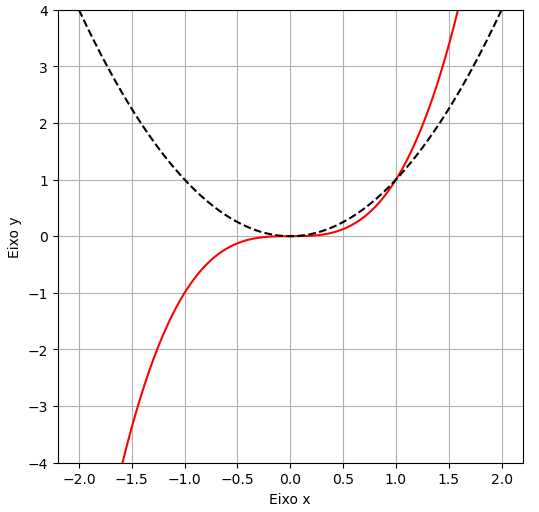
fig, ax = plt.subplots(figsize=(6,6),dpi=100)

x = np.linspace(-2,2,1000);

#Adicionando as labels (Nomes) dos gráficos
ax.plot(x,x**3,'r-',label='Função cúbica');
ax.plot(x,x**2,'k--',label='Função quadrática')

ax.set_xlabel('Eixo x');
ax.set_ylabel('Eixo y');
ax.set_ylim(-4,4);
ax.grid(True);

ax.legend(loc=3); #Imprimindo a legenda

Tarefa 6: Função legend()

Refaça a Tarefa 5 utilizando a abordagem funcional e utilize a função plt.savefig('tarefa6.png',dpi=300) para salvar a sua figura.

Solução:

plt.figure(figsize=(6,6),dpi=100) #Criando a figura

plt.plot(x,x**3,'r-',label='Função cúbica');
plt.plot(x,x**2,'k--',label='Função quadrática')

plt.xlabel('Eixo x');
plt.ylabel('Eixo y');
plt.ylim(-4,4);
plt.grid(True);

plt.legend(loc=3); #Imprimindo a legenda
plt.savefig('tarefa6.png',dpi=300)

Exemplo 7: Sub-gráficos (Subplots)

Podemos criar sub-gráficos através dos argumentos nrow e ncols. Neste caso a função irá retornar uma array de eixos.

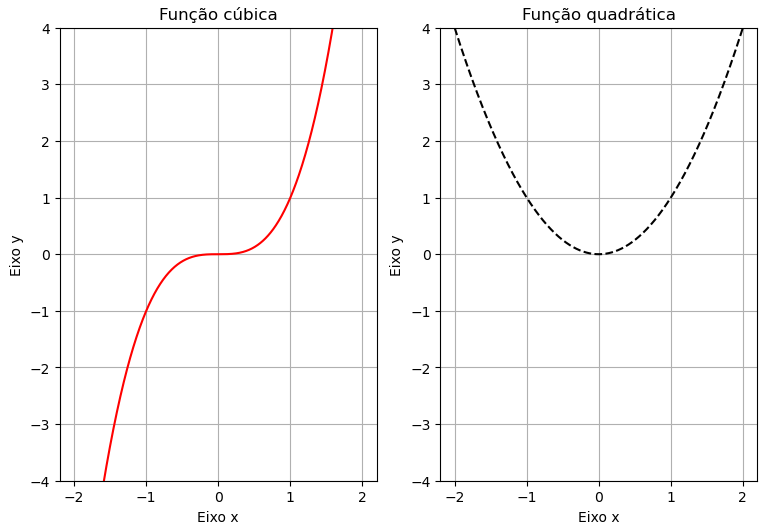
Vamos plotar os mesmos gráficos em sub-figuras separadas:

fig, axs = plt.subplots(figsize=(9,6),dpi=100,nrows=1,ncols=2)

#display(axs)

x = np.linspace(-2,2,1000);

axs[0].plot(x,x**3,'r-');
axs[1].plot(x,x**2,'k--');

Titulos=['cúbica','quadrática']

#Como ax é um array de eixos, podemos iterar no array
for i, ax in enumerate(axs):
    ax.set_xlabel('Eixo x');
    ax.set_ylabel('Eixo y');
    ax.set_ylim(-4,4);
    ax.grid(True);
    
    #Adicione o título no final
    ax.set_title(f'Função {Titulos[i]}')

Exemplo do subplots com mais de um eixo

Exemplo 9: Gráficos estatísticos

Existem muitos tipos de plotagem que podemos criar com o Matplotlib. Em relação aos gráficos estatísticos podemos considerar alguns exemplos:

Gráficos de dispersão:

Documentação

Para exemplificar o uso de dispersão vamos comparar duas amostras:

Vamos criar as amostras:

np.random.seed(200) #Selecionando um seed para reprodubilidade

qtd=100 #Tamanho das populações

# Amostra 1:
a1=np.random.rand(4,qtd)*100


# Amostra 2:
desvio_padrão=15
média=50

a2=média+desvio_padrão*np.random.randn(4,qtd);

#Concatenando as duas amostras em uma matriz 3D
a=np.concatenate((a1,a2),axis=0).reshape(2,4,qtd)

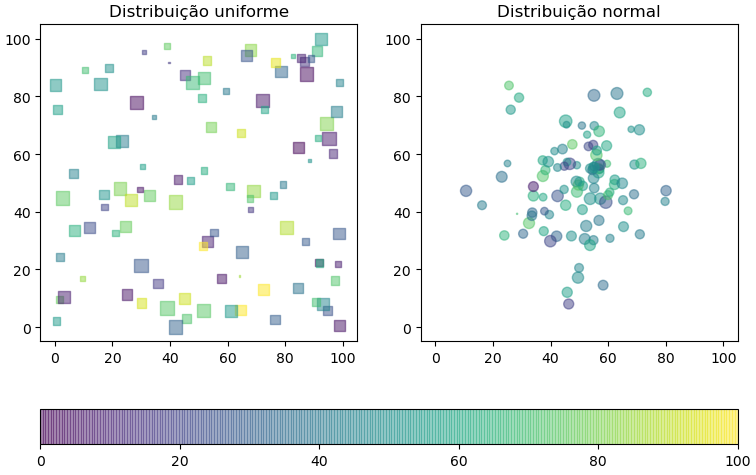
Plotando os gráficos:

fig, axs = plt.subplots(nrows=1,ncols=2,figsize=(9,6),dpi=100)

distribuição=['uniforme','normal']
marcador='so'

for i, ax in enumerate(axs):
    p=ax.scatter(a[i,0,:], #Valor de x
               a[i,1,:], #Valor de y
               c=a[i,2,:], #Cor
               s=a[i,3,:], #Área
               alpha=0.5, #Alfa
               vmin=0, #limite inferior das cores
               vmax=100, #limite superior das cores
               marker=marcador[i]
              )
    ax.set_xlim([-5,105])
    ax.set_ylim([-5,105])
    ax.set_title(f'Distribuição {distribuição[i]}')
    
#Adicionando uma colorbar
fig.colorbar(p, #Gráfico
             ax=axs, #Lista de eixos que a colorbar vai plotar
             orientation='horizontal' #Orientação fraction=0.05
             );

Grafico de dispersão

Histogramas

Documentação

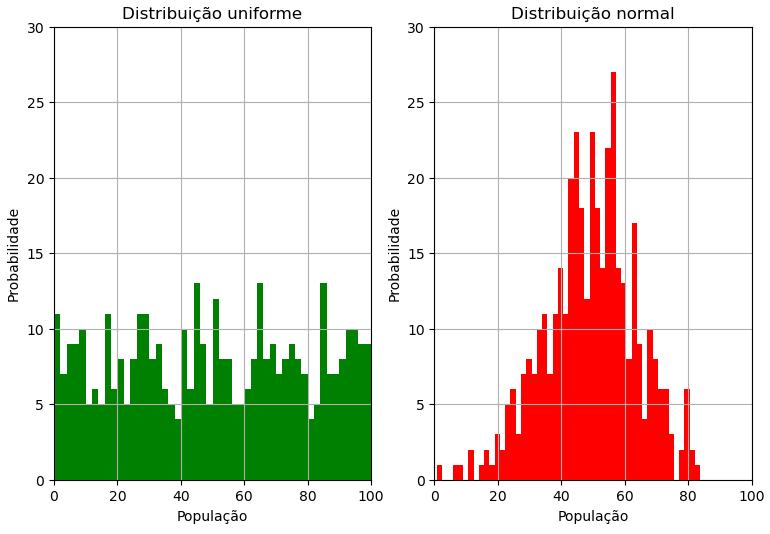
Vamos analisar nossas duas amostras utilizando o método hist().

fig, axs = plt.subplots(nrows=1,ncols=2,figsize=(9,6),dpi=100)

cores='gr'

for i, ax in enumerate(axs):
    #Transforma o array de 4x100 em 400x1
    amostras=a[i,:,:].reshape(a[i,:,:].size,1);
    
    ax.hist(amostras, #Amostras da minha população
                bins=50, #Quantidade de intervalos
                facecolor=cores[i] #cor
               );
    ax.grid(True)
    ax.set_xlim(0,100)
    ax.set_ylim(0,30)
    ax.set_xlabel('População');
    ax.set_ylabel('Probabilidade')
    ax.set_title(f'Distribuição {distribuição[i]}');

Histograma

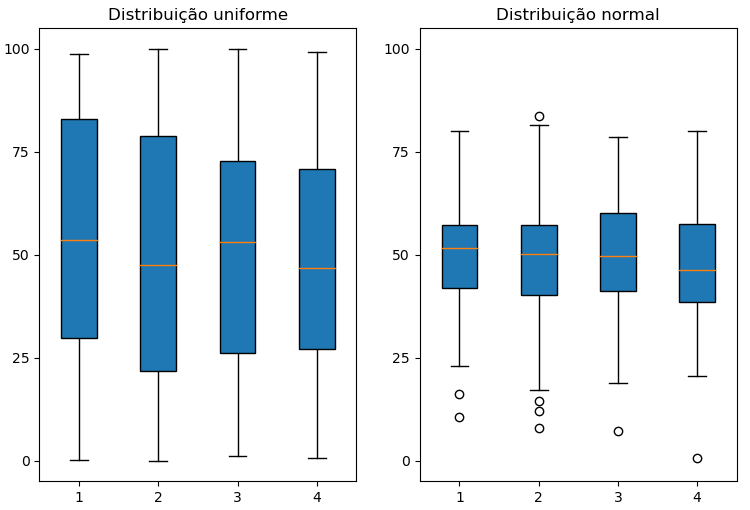
Diagrama de extremos e quartis:

Documentação

fig, axs = plt.subplots(nrows=1,ncols=2,figsize=(9,6),dpi=100)

for i, ax in enumerate(axs):
    ax.boxplot(a[i,:,:].T, #Amostra (Ou conjunto de amostras)
               vert=True, #Modo vertical
               patch_artist=True #Estilo do gráfico (True deixa mais bonito)
              );
    ax.set_ylim(-5,105);
    ax.set_title(f'Distribuição {distribuição[i]}');
    
    ax.set_yticks(np.arange(0,110,25));

Diagrama de extremos e quartis

Exemplo 10: Outros tipos de gráficos

Além dos gráficos estatísticos, o numpy permite criar outros tipos de gráficos. Segue alguns exemplos:

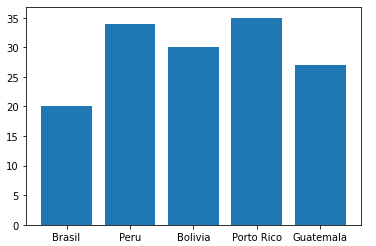
Para exemplificar veja como é feito um gráfico de barras super simples:

Dados = np.array([20, 34, 30, 35, 27])

x = np.arange(Dados.size)
plt.bar(x, Dados);
plt.xticks(x,('Brasil', 'Peru', 'Bolivia', 'Porto Rico', 'Guatemala'));

Gráfico de barras

Exemplo 11: Visualização de dados incorporada ao Pandas

O pandas tem uma série de métodos que permitem a visualização de dados. Neste exemplo veremos algumas delas.

Inicialmente iremos importar o pandas:

import pandas as pd

Histograma:

Agora vamos importar nosso primeiro dataframe utilizando o arquivo paises.csv:

df1 = pd.read_csv("paises.csv", #Nome do dataframe
                  index_col=0 #selecionando a coluna Name
                 )

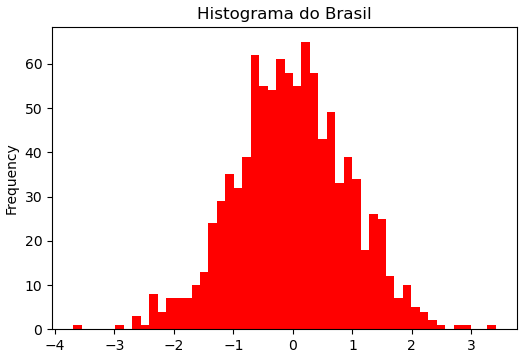
Deste dataframe vamos visualizar os dados do Brasil.

plt.figure(figsize=(6,4),dpi=100);
df1["Brasil"].plot.hist(bins=50,facecolor='r'); #Posso usar .hist também
plt.title('Histograma do Brasil');

Histograma com o pandas

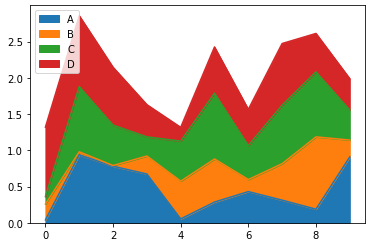
Area:

Para exemplificar o plot de área vamos utilizar como exemplo o arquivo experimento.csv.

Importando o dataframe:

df2=pd.read_csv('experimento.csv')

Plotando o gráfico:

df2.plot.area();

Gráfico de area com o pandas

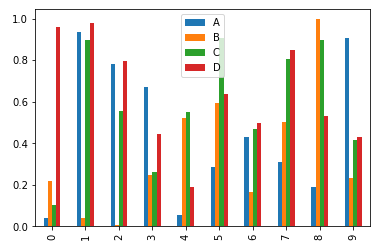
Gráficos de barras:

Usando o mesmo dataframe anterior:

df2.plot.bar();

Gráfico de barras com o pandas

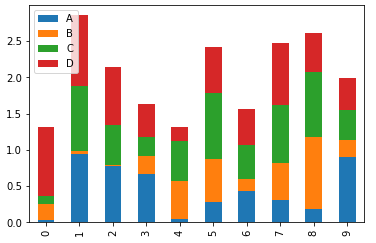
Colocando todos na mesma barra:

df2.plot.bar(stacked=True);

Gráfico de barras estacado

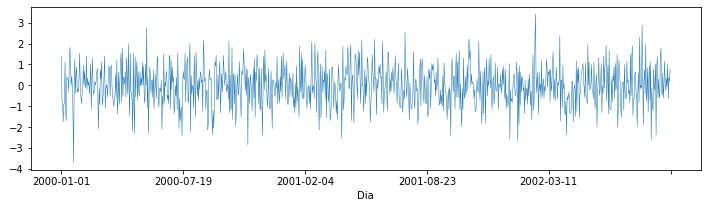
Gráfico de linhas:

df1['Brasil'].plot.line(linewidth=0.5,figsize=(12,3));

Gráfico de linha utilizando o pandas

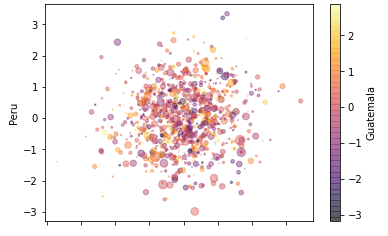
Grático de dispersão:

df1.plot.scatter(x='Brasil',y='Peru',c='Guatemala', s=(df1['Porto Rico'])**2*10,
                 cmap='inferno', #Define o estilo de cor
                 alpha=0.4);

Gráfico de dispersão usando o pandas

Diagrama de extremos e quartis:

df1.plot.box();

image-20201211024149734

Exemplo 12: SciPy e funções especiais

A bibliteca scipy tem uma coleção de algoritmos matemáticos e funções de conviniências construída sobre o Numpy. A documentação do SciPy é composta de várias seções, cujo o link está abaixo:

https://docs.scipy.org/doc/scipy/reference/

Nela podemos destacar alguns sub-módulos:

Dentre estes submódulos, vamos utilizar o submódulo scipy.signal para plotar algumas funções especiais.

Importando a biblioteca:

from scipy import signal

Criando o vetor de tempo:

t = np.linspace(-1, 1,10000);

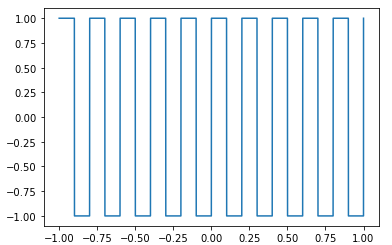
Onda quadrada:

y = signal.square(2*np.pi*5*t);
plt.plot(t,y);

Exemplo de uma onda quadrada

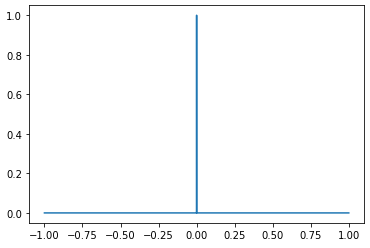
Impulso unitário:

y = signal.unit_impulse(t.size,int(t.size/2)); #Impulso em 0
plt.plot(t,y);

Exemplo de resposta ao impulso

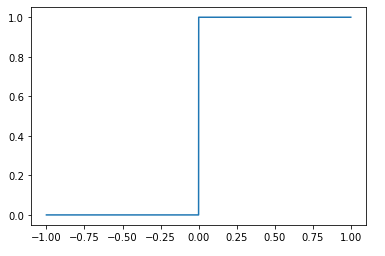
Degrau unitário:

y = np.heaviside(t,0); #Degrau
plt.plot(t,y);

Exemplo de resposta ao degrau

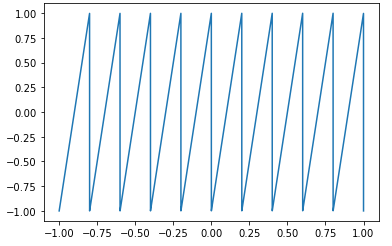
Onda dente de serra:

y=signal.sawtooth(2 * np.pi * 5 * t);
plt.plot(t,y);

Onda dente de serra

Exemplo 13: Matplotlib e Widgets

Para adicionar a possibilidade de interatividade no Matplotlib pode-se usar o comando mágico:

%matplotlib widget

Entretanto para adicionar essa possibilidade é necessário instalar a extensão:

jupyter-matplotlib

E instalar o pacote:

conda install -c conda-forge ipympl

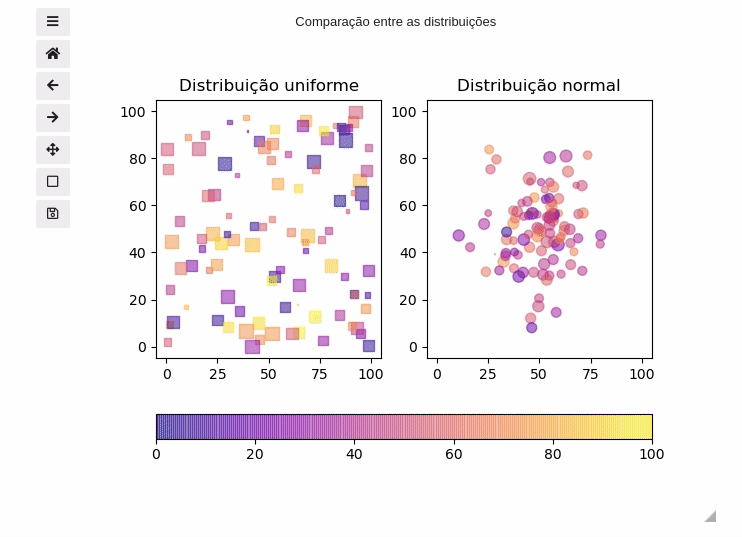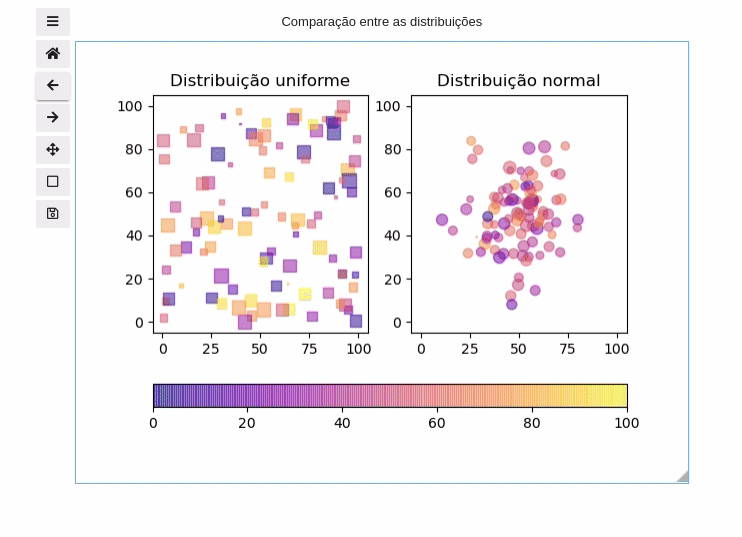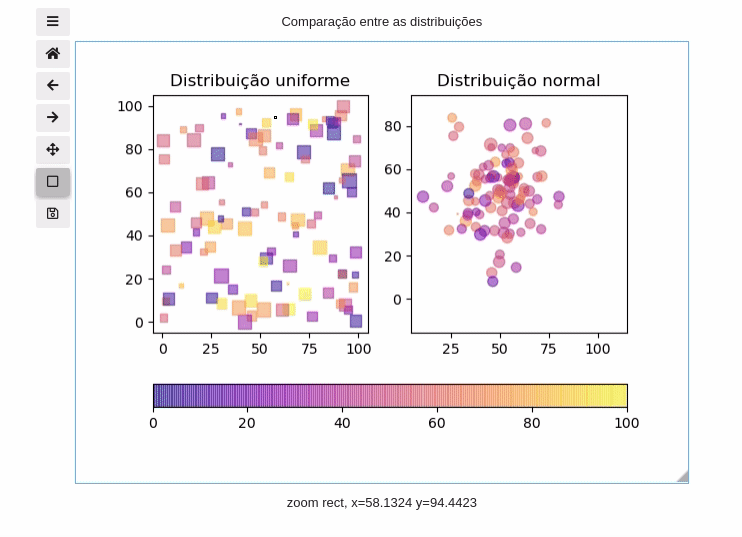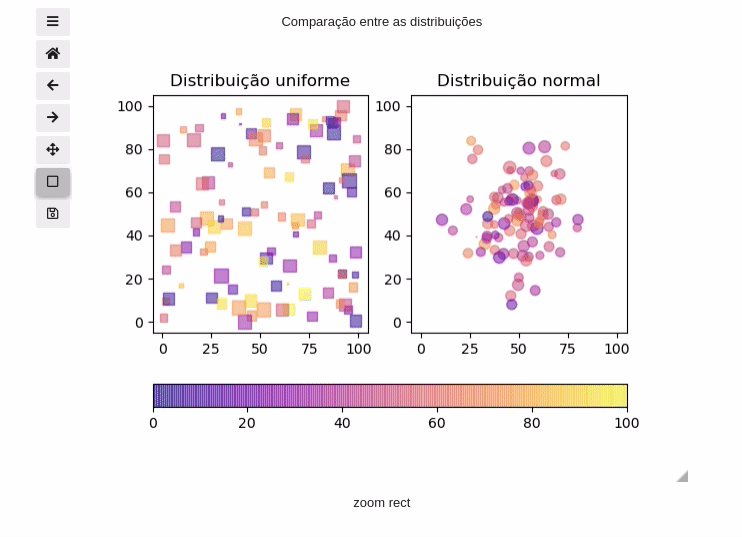
Ao adicionar o comando mágico na célula em que o gráfico é adicionado um widget que permite controlar o gráfico. Veja o exemplo abaixo:

%matplotlib widget
fig, axs = plt.subplots(nrows=1,ncols=2,
                        num='Comparação entre as distribuições' #Adiciono um nome à figura
                       )

distribuição=['uniforme','normal']
marcador='so'

for i, ax in enumerate(axs):
    p=ax.scatter(a[i,0,:], #Valor de x
               a[i,1,:], #Valor de y
               c=a[i,2,:], #Cor
               s=a[i,3,:], #Área
               alpha=0.5, #Alfa
               vmin=0, #limite inferior das cores
               vmax=100, #limite superior das cores
               marker=marcador[i],
               cmap='plasma' #Mudando o cmap para plasma
              )
    ax.set_xlim([-5,105])
    ax.set_ylim([-5,105])
    ax.set_title(f'Distribuição {distribuição[i]}')
    
#Adicionando uma colorbar
fig.colorbar(p, #Gráfico
             ax=axs, #Lista de eixos que a colorbar vai plotar
             orientation='horizontal' #Orientação fraction=0.05
             );

Uso de widgets no Matplotlib

Atividade 3: Projeto final

Neste momento chegamos ao final do curso, desta forma vocês estão capacitados para criar suas próprias aplicações. Sugere-se que faça algo simples utilizando o conhecimento adquirido durante as aulas. Segue algumas sugestões:

No final da próxima aula, caso haja voluntários disponibilizaremos espaço para àqueles que quiserem apresentar os seus projetos.

Dica: Para quem está interessado no Voilà siga este tutorial logo abaixo:

https://pythonforundergradengineers.com/deploy-jupyter-notebook-voila-heroku.html

ou visite esse Github:

https://github.com/voila-dashboards/voila-heroku