Neste capítulo será introduzido o uso do Python na computação cientítica. Apresentaremos algo leve como o cálculo diferencial e integral em conjunto com o Scipy e o Sympy, junto com o Sympy aprenderemos outros conceitos de funções. Posteriormente aprenderemos outras funções relevantes do Sympy e ao final aprenderemos a converter os Notebooks para:
- Arquivos de texto (PDF);
- Slides (Reveal);
- Aplicativos e slides dinâmicos (Voila+Reveal).
Atividade 1: Integral
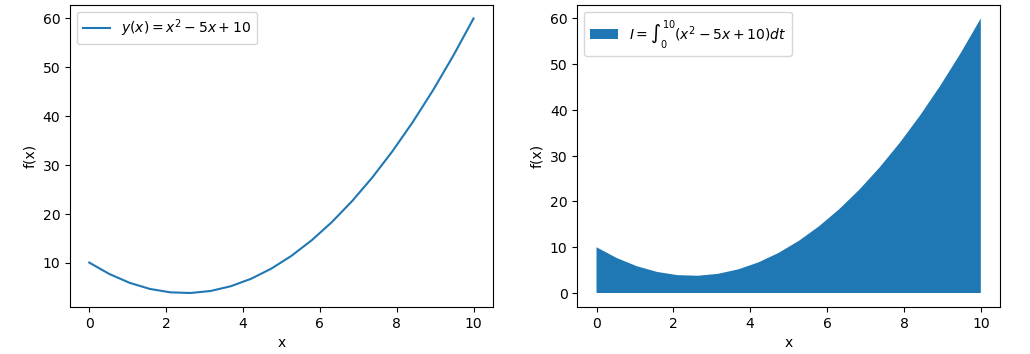
Por definição a integral $I(x)$ é a área em baixo da curva. O gráfico a esquerda é uma função quadrática $f(x)=x^2-5t+6$ e a integral desta função, $I$, corresponde à área em baixo da curva de $f(x)$, considerando um intervalo de 0 a 10:
# Importando as bibliotecas import numpy as np import matplotlib.pyplot as plt import matplotlib matplotlib.rc('figure',dpi = 100) #Modificando o valor padrão das figuras para 100 de dpi # Mais detalhes podem ser vistos aqui # https://matplotlib.org/tutorials/introductory/customizing.html#Criando os vetores x e y x = np.linspace(0,10,20) y = x**2 - 5*x + 10 #Criando uma figura com dois gráficos (duas colunas e uma linha) fig, axs = plt.subplots(nrows=1,ncols=2,figsize=(12,4)) # Usamos o método 'plot' para fazer plotagem em linha axs[0].plot(x,y,label="$y(x)=x^2-5x+10$"); # Usamos o método `fill_between` para plotagem em ÁREA # Documentação: https://matplotlib.org/3.3.3/api/_as_gen/matplotlib.pyplot.fill_between.html axs[1].fill_between(x,y,label=r"$I=\int_{0}^{10}\left(x^2-5x+10\right)dt$"); # Observe que utilizamos o modo raw (r) para escrever a fração no modo de equação: \frac{5}{2} #Adicionando alguns elementos no gráfico for ax in axs: ax.legend(loc="upper left") #legenda na parte superior esquerda ax.set_xlabel("x") ax.set_ylabel("f(x)")
O símbolo da integral é o “$\int$” e $a$ e $b$ são os intervalos de integração.
\[I=\int_{a}^{b}f(x)dt\]No nosso caso $a=0$ e $b=10$ e $y(x)=x^2 - 5x + 10$.
Resolver a integral de um polinômio é a mesma coisa que resolver indidualmente as integrais. Além disso, as constantes podem sair para fora da integral:
\[I=\int_{0}^{10}\left(x^2-5x+10\right)=\int_{0}^{10}x^2dx-5\int_{0}^{10}xdx+10\int_{0}^{10}dx\]Ao resolver cada uma das integrais individualmente temos:
\[I=\left[\frac{x^3}{3}-5\frac{x^2}{2}+10x\right]_0^{10}\]Para encontrar o valor numérico da área devemos substituir os limites de integração no valor de $x$. Sempre subtraindo o intervalo final, $a=10$, do inicial $b=0$:
\(I=\left[\frac{10^3}{3}-5\frac{10^2}{2}+10\cdot10\right]-\left[\frac{0^3}{3}-5\frac{x^2}{2}+10\cdot 0\right]=\frac{550}{3}\) Logo a área abaixo da curva é: \(I=\frac{550}{3}\)
Parte 1: Integração analítica com o Sympy
O Python permite o cálculo analítico da integral utilizando as funções do pacote Sympy utilizando variáveis simbólicas. Já trabalhamos com este pacote anteriormente na plotagem de gráficos.
# Importando sympy import sympy as sym# Antes de proceguir vamos criar funções que irá facilitar a nossa vida import IPython def md(txt): """ Mostra um texto em Markdown """ display(IPython.display.Markdown(txt)) def Eqn(eq): """ Função de equação centralizada e com numeração """ return md(r"\begin{equation}"+eq+r"\end{equation}")
Exemplo 1: Integral definida
Para resolver a integral utilizamos a função integrate. Nela podemos resolver integrais indefinidas (Os limites de integração não são definidos) ou definidas (Os limites de integração são definidos). E ainda, para mostrar as expressões na saída Markdown podemos utilizar a função latex:
\[x^{2} - 5 x + 10\]# Definindo a função f(x) x = sym.symbols('x') y = x**2-5*x+10 # Mostrando a equação na forma de Markdown Eqn(f'y(x)={sym.latex(y)}')# Resolvendo a integral indefinida I = sym.integrate(y)\[I(x)=\int \left(x^{2} - 5 x + 10\right)\, dx=\frac{x^{3}}{3} - \frac{5 x^{2}}{2} + 10 x+c\]# Mostrando o resultado na forma de Markdown Eqn(f'I(x)={sym.latex(sym.Integral(y))}={sym.latex(I)}+c') # A função 'Integral' permite mostrar a operação de integral sem resolve-la
Alternativamente, podemos utilizar o método doit para resolver a integral:
\[y(x)=x^{2} - 5 x + 10\] \[I(x)=\int \left(x^{2} - 5 x + 10\right)\, dx=\frac{x^{3}}{3} - \frac{5 x^{2}}{2} + 10 x+c\]x = sym.symbols('x') y = x**2-5*x+10 # Mostrando a equação na forma de Markdown Eqn(f'y(x)={sym.latex(y)}') #Resolvendo a integral Int=sym.Integral(y) #Definindo a integral Eqn(f'I(x)={sym.latex(Int)}={sym.latex(Int.doit())}+c')
O sympy permite resolver integrais complexas de forma analítica.
Tarefa 1: Utilizando o Sympy e as saídas do IPython resolva as integrais das seguintes funções: \(y(x)=\sqrt{x + 1}\)
\[y(x)=\frac{x^{2} - 3 x + 5}{3 x^{3} + x^{2} + x}\]\[y(x)=\sqrt{x + 1}\]#Tarefa: Resolva as integrais usando o Sympy y2 = sym.sqrt(1+x) # Definindo a função Int2=sym.Integral(y2) # Definindo a integral Eqn(f'y(x)={sym.latex(y2)}') Eqn(f'I(x)={sym.latex(Int2)}={sym.latex(Int2.doit())}+c')\(I(x)=\int \sqrt{x + 1}\, dx=\frac{2 \left(x + 1\right)^{\frac{3}{2}}}{3}+c\)
\[y(x)=\frac{x^{2} - 3 x + 5}{3 x^{3} + x^{2} + x}\] \[I(x)=\int \frac{x^{2} - 3 x + 5}{3 x^{3} + x^{2} + x}\, dx=5 \log{\left(x \right)} - \frac{7 \log{\left(x^{2} + \frac{x}{3} + \frac{1}{3} \right)}}{3} - \frac{34 \sqrt{11} \operatorname{atan}{\left(\frac{6 \sqrt{11} x}{11} + \frac{\sqrt{11}}{11} \right)}}{33}+c\]y3 = (x**2-3*x+5)/(3*x**3+x**2+x) Eqn(f'y(x)={sym.latex(y3)}') Eqn(f'I(x)={sym.latex(sym.Integral(y3))}={sym.latex(sym.integrate(y3))}+c')
Exemplo 2: Integrais definidas
Podemos atribuir um intervalo de integração a nossa integral adicionando uma tupla com as variáveis e os limites de integração superior e inferior:
integrate(f(x),(x,a,b))
onde $a$ e $b$ são os limites inferior e superior, respectivamente.
a=0 # Limite inferior b=10 # Limite superior md(f'Vamos tentar resolver a integral de $y(x)={sym.latex(y)}$ considerando os intervalos de ${a}$ a ${b}$:')Vamos tentar resolver a integral de $y(x)=x^{2} - 5 x + 10$ considerando os intervalos de $0$ a $10$:
\[I(x)=\int\limits_{0}^{10} \left(x^{2} - 5 x + 10\right)\, dx=\left[\frac{x^{3}}{3} - \frac{5 x^{2}}{2} + 10 x\right]_0^{10}=\frac{550}{3}\]I=sym.integrate(y) Int=sym.Integral(y,(x,a,b)) Eqn(fr'I(x)={sym.latex(Int)}=\left[{sym.latex(I)}\right]_{a}^{{{b}}}={sym.latex(Int.doit())}')
Parte 2: Integração numérica
Além da integração analítica é possível calcular a integral através de métodos numéricos. Este método é especialmente útil quando a função não é integrável ou quando a função não é definida matemáticamente. Inicialmente vamos apresentar alguns métodos de integração e posteriormente vamos utilizar este conceito em um problema prático.
Exemplo 3: Regra trapezoidal
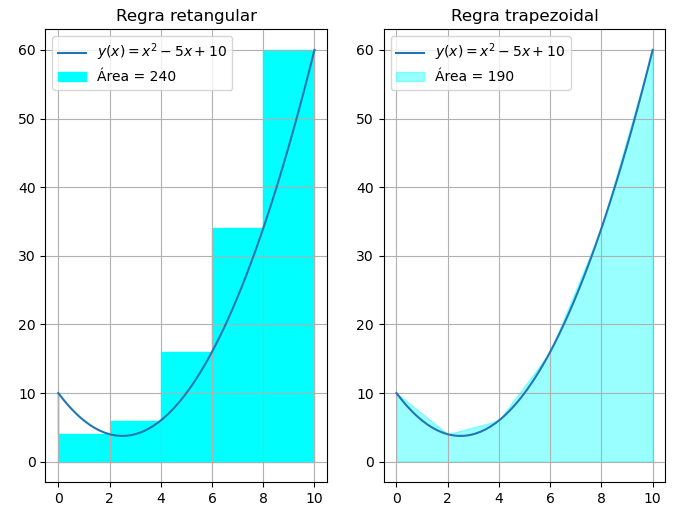
Mas como calcular a integral deste gráfico se não temos uma função definida. Neste caso podemos utilizar técnicas de integração númerica. Como a regra do retangular e trapezoidal apresentada gráficamente na figura abaixo:
#Criando os vetores x e y x = np.linspace(0,10) y = x**2 - 5*x + 10 # Criando vetores para demonstrar a integração numérica xi = np.arange(0,11,2) yi = xi**2 - 5*xi + 10 fig, axs = plt.subplots(nrows=1,ncols=2,figsize=(8,6)) Títulos = ['retangular','trapezoidal'] for j, ax in enumerate(axs): if j==0: ax.fill_between(xi,yi,step='pre',color='cyan',label=f'Área = {yi[1:].sum()*2:g}'); elif j==1: ax.fill_between(xi,0,yi,color='cyan',alpha=0.4,label=f'Área = {np.trapz(yi,xi):g}'); ax.plot(x,y,label="$y(x)=x^2-5x+10$"); ax.set_title(f'Regra {Títulos[j]}'); ax.legend(); ax.grid(True);
A regra retangular divide a figura em diversos retângulos e calcular a área destes retângulos (A esquerda). Embora simples, possui uma baixa precisão. Já a regra trapezoidal divide a figura em trapézios (A direita). Considerando os mesmos passos de integração, a regra trapezoidal tem uma precisão no cálculo da área muito superior.
O numpy permite o cálculo da área utilizando o método trapezoidal através da função trapz(y,[x],[dx]), cuja a documentação está disponível aqui.
md(f'Usando a função `trapz` o valor da integral é {np.trapz(yi,dx=xi[1]-xi[0]):g}, já com a regra retangular o valor da integral é {yi[1:].sum()*2}.')Usando a função
trapzo valor da integral é 190, já com a regra retangular o valor da integral é 240.
Caso haja necessidade de maior precisão, pode-se utilizar a regra de Simpson. Este método utiliza polinómios (de segundo grau) para fazer o cálculo da integral, como mostra a figura abaixo, retirada da Wikipédia:
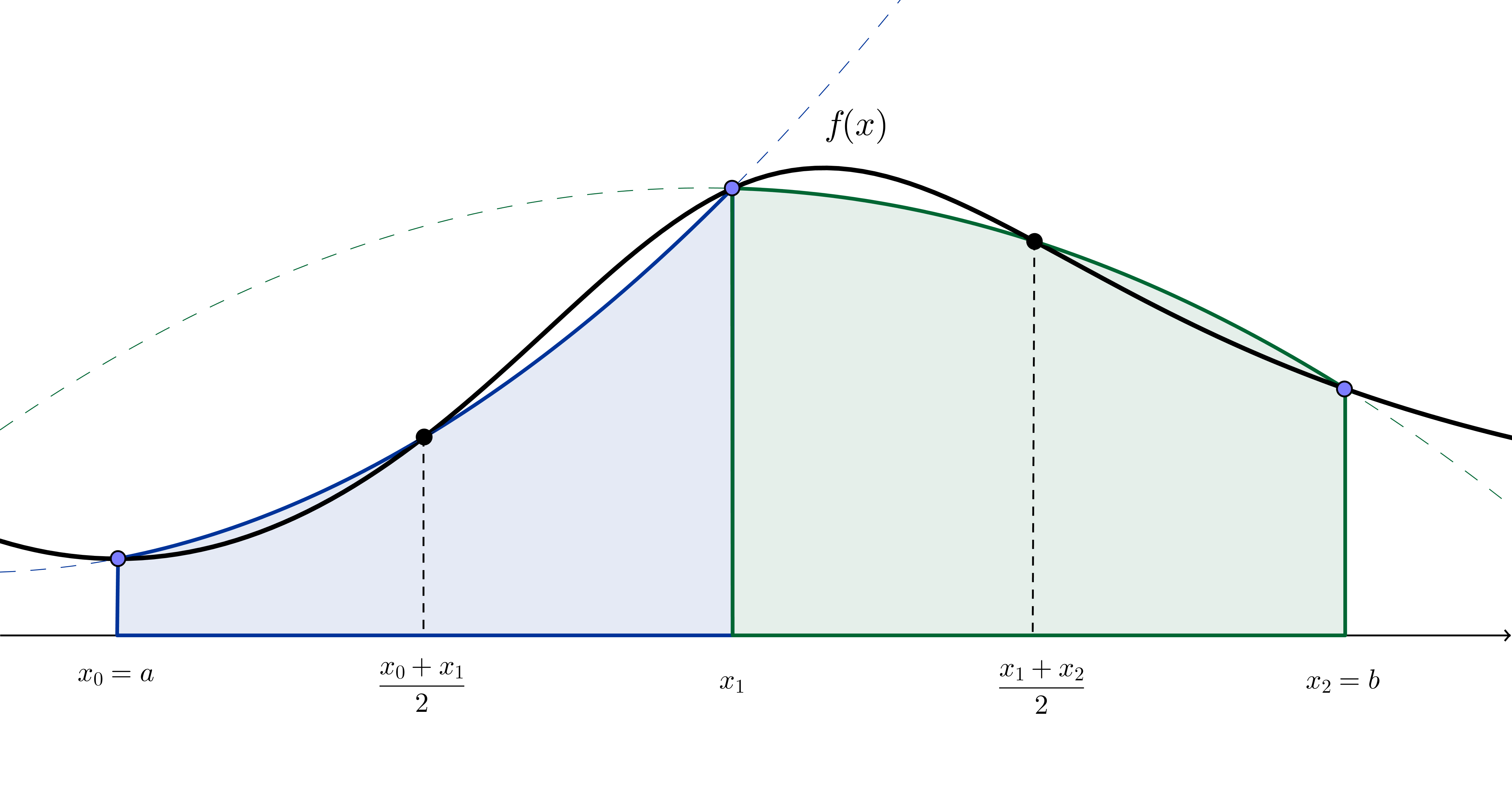
Para utilizar a regra de Simpson devemos recorrer a função simps(y,[x],[dx]) do sub-módulo integrate do scipy.
# Importando utilizando o sub-módulo de integração from scipy import integrate # Mostrando o resultado da integração md(f'De acordo com o `simp` o valor da área é {integrate.simps(yi,xi):.6g}, isso dá uma diferença de {abs(integrate.simps(yi,xi)-np.trapz(yi,xi))/integrate.simps(yi,xi)*100:.2}\% comparado com o `trapz`.')De acordo com o
simpo valor da área é 184.667, isso dá uma diferença de 2.9% comparado com otrapz.
Exemplo 4: Integração a partir de funções
Além dos métodos citados (Trapezoidal e Simpson) existem outros métodos mais precisos, como o método de quadratura e o método de Romberg. Ambos os métodos estão disponíveis através de funções do sub-módulo integrate através das funções quad e romberg.
Ao contrário das outras funções apresentadas anteriormente, que calculam a integral a partir de amostras, as funções quad e romberg calculam a integrais através de funções. A função quad, por exemplo, tem a seguinte sintaxe:
integral, erro_estimado = quad(
func, #Função
a, #limite inferior de integração
b #limite superior de integração
)
Para calcular a integral a partir deste método você deve definir a função previamente ou utilizar uma função anônima.
# Como o método de quadratura recebe uma função, ao invés de um vetor y é necessário criá-la def y(x): return x**2-5*x+10 # Agora podemos calcular o valor de integral I, erro = integrate.quad(y,0,10)# Alternativamente podemos utilizar uma 'função de uma anônima - 'anonymous function', desta forma, não precisamos declarar a função anteriormente I, erro = integrate.quad(lambda x: x**2-5*x+10, #Definição de uma função anônima (função de uma única linha) 0, #limite inferior 10 #limite superior ) md(f'Pelo método de quadratura a área do gráfico é {I:.4g} e pelo método de Romberg a integral é {integrate.romberg(lambda x: x**2-5*x+10,0,10):.4g}.')Pelo método de quadratura a área do gráfico é 183.3 e pelo método de Romberg a integral é 183.3.
Exemplo 5: Integração a partir de um arquivo csv
O cálculo da área do gráfico tem várias aplicações. Por exemplo, dada uma curva de velocidade em relação ao tempo, pode-se encontrar a distância percorrida através do cálculo da área do gráfico (A integral).
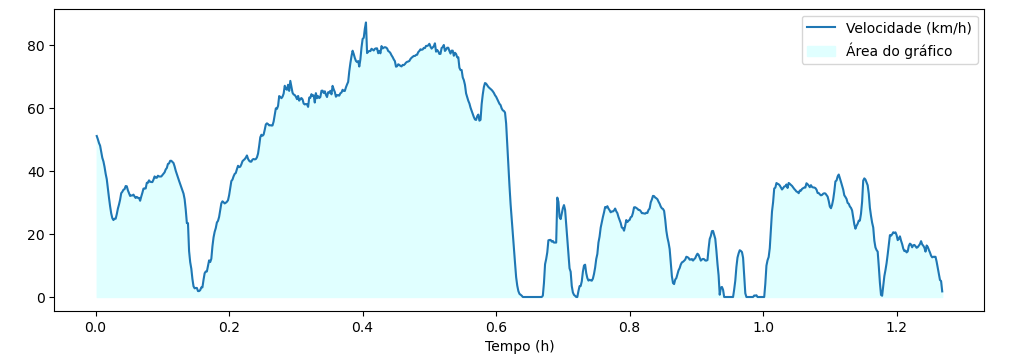
Considere que a velocidade de um veículo em um determinado percurso foi registrada e salva no arquivo velocidade.csv. Podemos importar este arquivo e mostrar o gráfico de velocidade em função do tempo.
#### Plotando o gráfico utilizando o numpy e matplotlib tempo, velocidade = np.loadtxt("velocidade.csv", unpack=True, #Permite que cada variável tem o seu valor correspondente delimiter=',', #Delimitador do arquivo csv skiprows=1 #Pula o cabeçalho (Primeira linha) ) plt.figure(figsize=(12,4)); plt.plot(tempo,velocidade,label='Velocidade (km/h)'); plt.fill_between(tempo,velocidade,color='lightcyan',label='Área do gráfico') plt.legend(); plt.xlabel('Tempo (h)');
#### Plotando o gráfico utilizando o pandas # import pandas as pd # df = pd.read_csv('velocidade.csv',index_col=0) #importa o csv e seleciona o tempo como índice # df.plot.line(figsize=(12,4)); #Plota o gráfico # plt.fill_between(df.index,df['Velocidade (km/h)'],color='lightcyan',label='Área do gráfico'); # plt.legend();d_simp=integrate.simps(velocidade,tempo) d_trap=integrate.trapz(velocidade,tempo) md(f"Utilizando o método de Simpson a distância percorrida pelo veículo foi de $A={d_simp:g}$ km. Pelo método trapezoidal a distância foi de $A={d_trap:g}$ km. E o erro entre os dois métodos foi de ${abs(d_simp-d_trap)*1000:g}$ m, que é relativamente pequena.")Utilizando o método de Simpson a distância percorrida pelo veículo foi de $A=45.1984$ km. Pelo método trapezoidal a distância foi de $A=45.2086$ km. E o erro entre os dois métodos foi de $10.2292$ m, que é relativamente pequena.
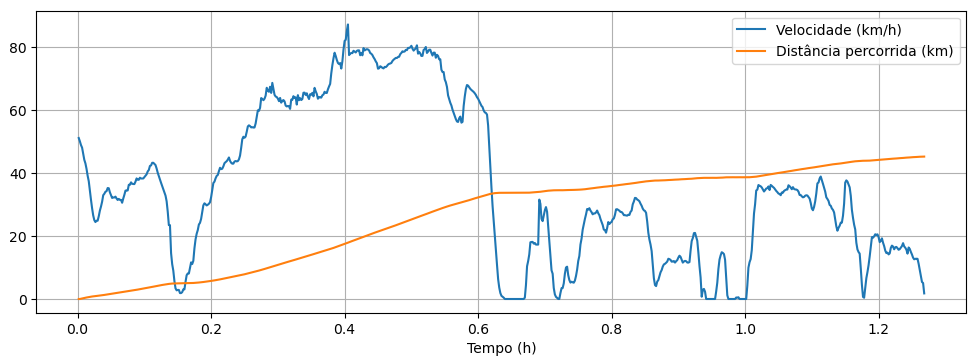
Podemos plotar o gráfico de distância percorrida, $d$, se variarmos o período de integração de $0$ a $t_0$:
\[d(t_0)=\int_0^{t_0} v(t) dt\]Com $t_0$ variando de um valor imediatamente superior a zero até o último valor do array de tempo. Além disso, por definição $d(0)=0$.
# Usando o list comprehension para criar array com t0 variando entre os valores de tempo d=np.array([0]+[integrate.simps(velocidade[:t0],tempo[:t0]) for t0 in range(1,tempo.size)])#Plotando o gráfico plt.figure(figsize=(12,4)); plt.plot(tempo,velocidade,label='Velocidade (km/h)'); plt.plot(tempo,d,label='Distância percorrida (km)'); plt.legend(); plt.xlabel('Tempo (h)'); plt.grid(True);
Atividade 2: Derivada
Derivada $f’(x)$ é a inclinação de uma reta tangente à uma curva $f(x)$. A reta tangente é demonstrada na figura abaixo retirada da Wikipédia:
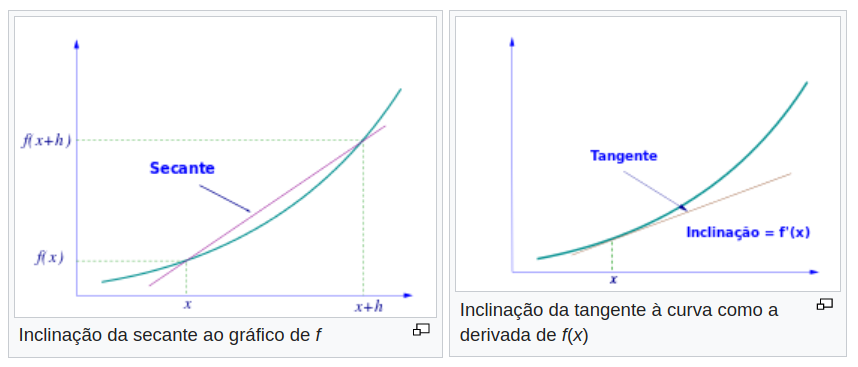
Em termos matemáticos a definição da derivada é dada por:
\[\frac{dy}{dx}=\lim_{h\rightarrow 0} \frac{y(x+h)-y(x)}{h}\]Parte 3: Derivada analítica com o Sympy
Exemplo 6: Primeira derivada
O sympy permite fazer o cálculo derivada de forma analítica através da função diff. Esta função tem os seguintes parâmetros:
diff(y(x),
[x], #Opcional
[ordem] #Opcional (Padrão 1)
)
Por exemplo, a derivada de:
# Definindo a função x=sym.symbols('x') y=x**2 - 5*x +10\[\frac{dy}{dx}=\frac{d}{d x} \left(x^{2} - 5 x + 10\right)=2 x - 5\]# Mostrando o resultado da derivada problema=sym.Derivative(y) derivada=sym.diff(y) Eqn(fr'\frac{{dy}}{{dx}}={sym.latex(problema)}={sym.latex(derivada)}') # Explicando o que faz cada função: # - A função Derivative mostra o valor da derivada não resolvida # - A função latex converte uma expressão no sympy para o formato de equação do latex
Ou ainda, pelo método doit:
\[\frac{dy}{dx}=\frac{d}{d x} \left(x^{2} - 5 x + 10\right)=2 x - 5\]problema=sym.Derivative(y) Eqn(fr'\frac{{dy}}{{dx}}={sym.latex(problema)}={sym.latex(problema.doit())}')
Para encontrar a derivada em um determinado ponto, podemos usar o método subs. O método subs tem a seguinte sintaxe:
subs(old, #Variaveis antigas (Pode ser uma tupla ou um escalar)
new #Variaveis novas (Pode ser uma tupla ou um escalar a variável pode ser simbólica ou não)
)
pto=3 md(f'Por exemplo, caso seja necessário achar o valor da derivada no ponto {pto}:') Eqn(fr"y'({pto})={sym.latex(derivada.subs(x,3))}")Por exemplo, caso seja necessário achar o valor da derivada no ponto 3: \(y'(3)=1\)
Caso queiramos a derivada de segunda ordem, podemos acrescentar um segundo parâmetro:
\[\frac{d^2}{dx^2}\left(x^{2} - 5 x + 10\right)=2\]# Mostrando o resultado da segunda derivada Eqn(fr'\frac{{d^2y}}{{dx^2}}\left({sym.latex(y)}\right)={sym.latex(sym.diff(y,x,2))}')
Exemplo 7: Lambdify
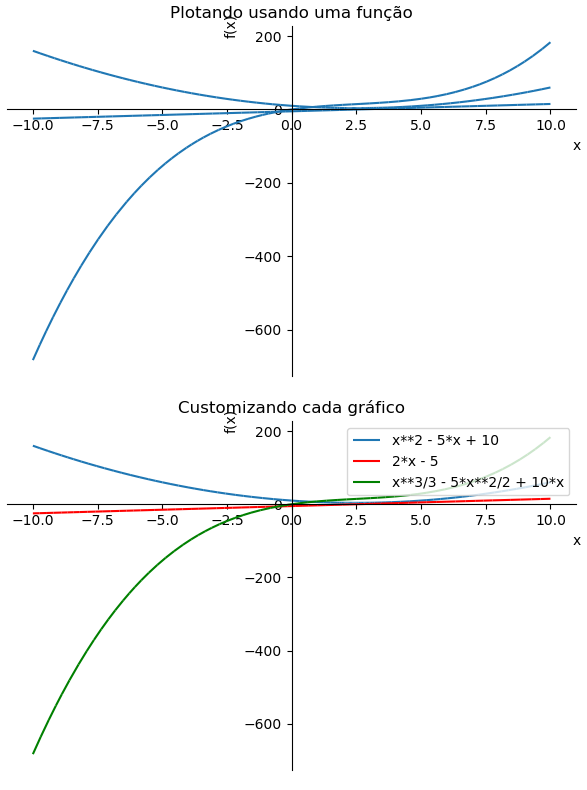
Vimos anteriormente como plotar o gráfico utilizando o Sympy, porém com pouca customização. Relembrando como era feita a plotagem utilizando o Sympy:
# Função x=sym.symbols('x') y = x**2 -5*x+10 dydx=y.diff() I=y.integrate() # Plotando na mesma função sym.plot(y,dydx,I,title='Plotando usando uma função') # Customizando cada gráfico p1=sym.plot(y,show=False,title='Customizando cada gráfico',legend=True) p2=sym.plot(dydx,line_color='r',show=False) p3=sym.plot(I,line_color='g',show=False) p1.extend(p2) p1.extend(p3) p1.show()
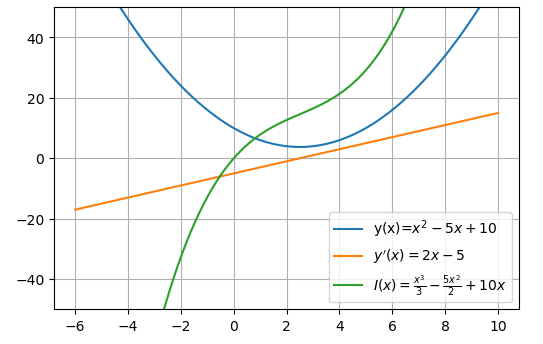
Entretando, a função de plotagem do Sympy não é muito flexível, ela é útil apenas para plotagens rápidas sem grandes customizações. Caso seja necessário uma customização maior podemos utilizar o Matplotlib. Para isso podemos utilizar a função lambdify do Sympy. Esta função transforma uma função do Sympy em uma função (lambda) do Python. A função tem a seguinte sintaxe:
lambdify(variáveis, #array ou escalar das variáveis da função
expressão, #Função propriamente dita
biblioteca #Biblioteca no qual a função deve ser convertida (Math ou numpy, por exemplo)
)
# Função x=sym.symbols('x') y = x**2 -5*x+10 dydx=y.diff() I=y.integrate() # Transformando as funções do Sympy em funções lambda (Inline function) yLamb=sym.lambdify(x,y,'numpy') dydxLamb=sym.lambdify(x,dydx,'numpy') ILamb=sym.lambdify(x,I,'numpy') #Criando o vetor x x=np.linspace(-6,10,100) #Plotando os gráficos plt.plot(x,yLamb(x),label=f'y(x)=${sym.latex(y)}$'); plt.plot(x,dydxLamb(x),label=f'$y\'(x)={sym.latex(dydx)}$'); plt.plot(x,ILamb(x),label=f'$I(x)={sym.latex(I)}$'); plt.grid(True); plt.ylim(-50,50); plt.legend();
Parte 4: Diferenciação numérica
Em algoritmos numéricos não é possível tender o $h$ tender a zero, logo devemos aproximar a derivada por:
\[\frac{dy}{dx}\approx\frac{\Delta y}{\Delta x}=\frac{y(x+h)-y(x)}{h}\]Neste caso, estamos trabalhando com a inclinação da reta secante.
Exemplo 8: Métodos avançar e retroceder
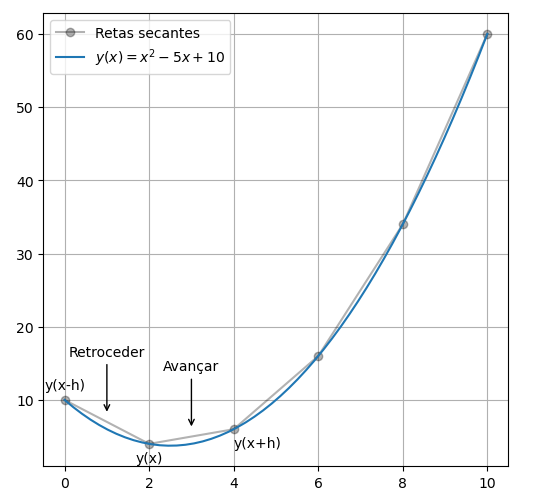
Existem dois métodos de cálculo da derivada:
- Método avançar (forward) \(\frac{dy}{dx}\approx\frac{y(x+h)-y(x)}{h}\)
- Método retroceder (backward)
### Criando os vetores x e y x = np.linspace(0,10) f = lambda x: x**2 - 5*x + 10 #Criando uma inline function para ser utilizada posteriormente # Definindo o vetor y y = f(x) ### Criando vetores para demonstrar as retas secantes xi = np.arange(0,11,2) yi = f(xi) ### Plotando os gráficos fig, ax = plt.subplots(figsize=(6,6)) ax.plot(xi,yi,'-o',label='Retas secantes',alpha=0.3,color='black'); ax.plot(x,y,label="$y(x)=x^2-5x+10$"); ax.legend(); ax.grid(True); ### Adicionando textos Pontos = ('y(x-h)','y(x)','y(x+h)') # Customizações do texto (Alinhamento) # Mais informações: https://matplotlib.org/3.1.1/tutorials/text/text_props.html Alinhamento = ({'ha': 'center', 'va': 'bottom'}, #y(x-h) {'ha': 'center', 'va': 'top'}, #y(x) {'ha': 'left', 'va': 'top'} #y(x+h) ) for i in range(3): #Adicionando os pontos ax.text(xi[i],yi[i]+(-1)**bool(i), #Posição Pontos[i], #Textos Alinhamento[i] #Parâmetros ) ### Adicinando anotações # Mais informações: https://matplotlib.org/3.3.3/tutorials/text/annotations.html Textos=['Retroceder','Avançar'] for x in [1,3]: ax.annotate(Textos[int((x-1)/2)], #Textos xy=(x,f(x)+2), #Posição final da seta xytext=(x,f(x)+10), #Posição do texto textcoords='data', ha='center', arrowprops=dict(arrowstyle="->",facecolor='black') #Parâmetros )
# Criando uma função de derivada
def dydx(fun,a=0,h=0.01,Método="Avanço"):
"""
Função que calcula a derivada:
fun <- Função
a <- Ponto (Padrão = 0)
h <-dx (Padrão = 2)
Método <- Avanço ou retroceder (Padrão = avanço)
"""
if Método=="Avanço":
return (fun(a+h)-fun(a))/h
else:
return (fun(a)-fun(a-h))/h
Teste essa função com vários valores.
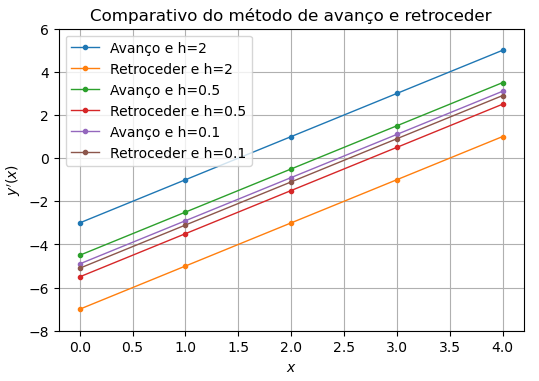
#Criando uma inline function para ser a nossa função y = lambda x: x**2 - 5*x + 10 #Criando um DataFrame import pandas as pd resultados = pd.DataFrame(index=np.arange(0,5,1)) #Os índices são os pontos #Preenchendo o dataframe hs=[2,0.5,0.1] Métodos=["Avanço","Retroceder"] for h in hs: for Método in Métodos: resultados[f"{Método} e h={h}"]=dydx(y,a=resultados.index,h=h,Método=Método) md(resultados.to_markdown())
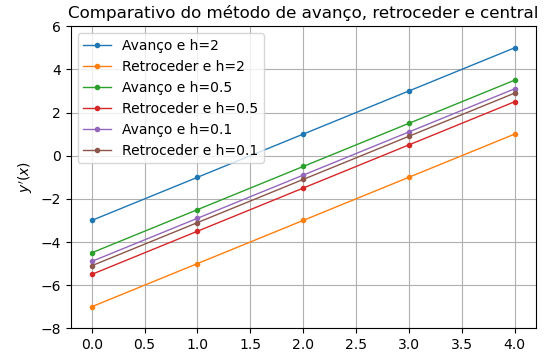
Avanço e h=2 Retroceder e h=2 Avanço e h=0.5 Retroceder e h=0.5 Avanço e h=0.1 Retroceder e h=0.1 0 -3 -7 -4.5 -5.5 -4.9 -5.1 1 -1 -5 -2.5 -3.5 -2.9 -3.1 2 1 -3 -0.5 -1.5 -0.9 -1.1 3 3 -1 1.5 0.5 1.1 0.9 4 5 1 3.5 2.5 3.1 2.9 resultados.index.name="$x$" resultados.plot(lw=1,marker='.'); plt.grid(); plt.ylabel("$y'(x)$"); plt.title("Comparativo do método de avanço e retroceder"); plt.ylim(-8,6);
Se analisarmos graficamente, percebemos que o método avanço sempre tem um erro ‘positivo’ e o método atraso tem um erro ‘negativo’.
Exemplo 9: Método central
Para aumentar a precisão da derivada podemos utilizar um método que combina tanto o método avançar, quanto o método retroceder, o método central:
\[\frac{dy}{dx}\approx\frac{y(x+h/2)-y(x-h/2)}{h}=\frac{y(x+h)-y(x-h)}{2h}\]# Vamos modificar a nossa função de derivada e incluir o método central def dydx(fun,a=0,h=0.01,Método="Central"): """ Função que calcula a derivada: fun <- Função a <- Ponto (Padrão = 0) h <-dx (Padrão = 2) Método <- Avanço ou retroceder (Padrão = avanço) """ if Método=="Avanço": return (fun(a+h)-fun(a))/h elif Método=="Retroceder": return (fun(a)-fun(a-h))/h else: #Método central return (fun(a+h)-fun(a-h))/(2*h)# Adicionando mais uma coluna no Dataframe resultados["Central e h=2"]=dydx(y,a=resultados.index,h=2,Método="Central")#Plotando o gráfico resultante md(resultados.to_markdown()) resultados.plot(lw=1,marker='.'); plt.grid(); plt.ylabel("$y'(x)$"); plt.title("Comparativo do método de avanço, retroceder e central"); plt.ylim(-8,6);
Avanço e h=2 Retroceder e h=2 Avanço e h=0.5 Retroceder e h=0.5 Avanço e h=0.1 Retroceder e h=0.1 0 -3 -7 -4.5 -5.5 -4.9 -5.1 1 -1 -5 -2.5 -3.5 -2.9 -3.1 2 1 -3 -0.5 -1.5 -0.9 -1.1 3 3 -1 1.5 0.5 1.1 0.9 4 5 1 3.5 2.5 3.1 2.9
Observe que mesmo com um valor de $h$ grande o método retroceder trouxe bons resultados.
Finalmente, podemos utilizar a função derivative do submódulo misc do Scipy, que tem a seguinte sintaxe:
derivative(func,#função
x0,#Ponto
[dx]#Valor de h (opcional, padrão 1)
)
# Adicionando mais uma coluna no Dataframe from scipy import misc resultados["Scipy"]=misc.derivative(y,resultados.index) md(resultados.to_markdown())
Avanço e h=2 Retroceder e h=2 Avanço e h=0.5 Retroceder e h=0.5 Avanço e h=0.1 Retroceder e h=0.1 Scipy 0 -3 -7 -4.5 -5.5 -4.9 -5.1 -5 1 -1 -5 -2.5 -3.5 -2.9 -3.1 -3 2 1 -3 -0.5 -1.5 -0.9 -1.1 -1 3 3 -1 1.5 0.5 1.1 0.9 1 4 5 1 3.5 2.5 3.1 2.9 3
Exemplo 10: Derivada a partir de um arquivo csv
A integral da velocidade fornece a distância percorrida. A aceleração é a derivada em função do tempo:
\[a=\frac{dv}{dt}\]Assim, como a integral a derivada também tem um significado físico. Para encontrar o valor da derivada podemos utilizar diretamente a definição do método central:
\[\frac{dv}{dt}\approx\frac{v(t+h)-v(t-h)}{2h}\]Neste caso o valor de $h$ é o período de amostragem de $t$, ou seja h=t[1]-t[0].
Como a distância $h$ é o próprio período de amostragem, logo podemos trabalhar a diferença das velocidades diretamente com os índices. Assim a derivada resulta em:
\[\frac{dv}{dt}\approx\frac{v[k+1]-v[k-1]}{2(t[1]-t[0])}\]Onde $k$ é um vetor de índice do vetor de tempo.
Podemos calcular o método avanço ou retroceder utilizando o fatiamento de arrays. No caso do método de avanço: \(\frac{dv}{dt}\approx\frac{v[k+1]-v[k]}{2h}\)
O gráfico abaixo compara os dois métodos:
h2=2*(tempo[1]-tempo[0]) #Calculando previamente o valor de 2h dvdt_m=np.array([(velocidade[k+1]-velocidade[k-1])/h2 for k in range(1,tempo.size-1)]) #filt=signal.sosfilt(sos, dvdt) # Podemos obter o mesmo resultado através do fatiamento de arrays dvdt_a=(velocidade[1:]-velocidade[:-1])/(tempo[1]-tempo[0])
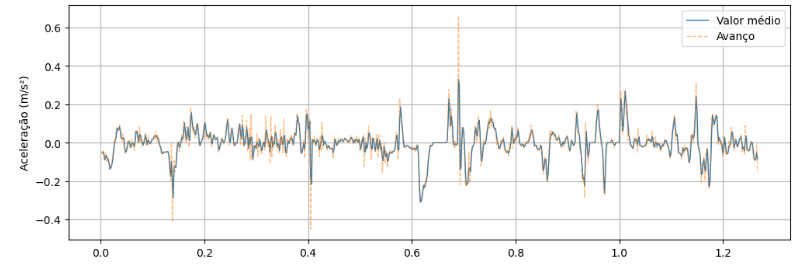
O gráfico abaixo compara os dois métodos:
kmh2toms2=1000/(3600**2) plt.figure(figsize=(12,4)); plt.plot(tempo[1:-1],dvdt_m*kmh2toms2,label='Valor médio',lw=1); plt.plot(tempo[:-1],dvdt_a*kmh2toms2,'--',label='Avanço',alpha=0.5,lw=1); plt.legend(); plt.ylabel('Aceleração (m/s²)') plt.grid(True);
Observe que o método do valor médio é mais preciso e apresenta “picos” menores.
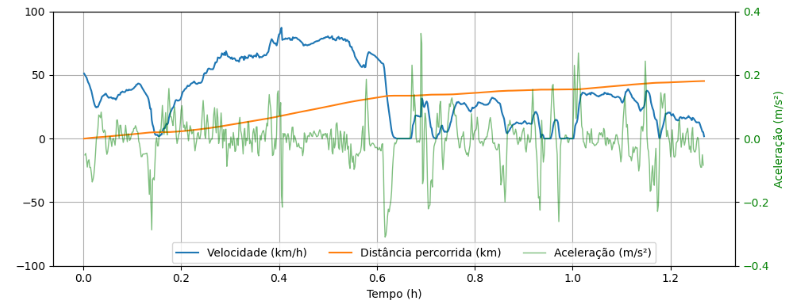
Comparando os gráficos:
fig, ax1 = plt.subplots(figsize=(10,4)); ax1.plot(tempo,velocidade,label='Velocidade (km/h)'); ax1.plot(tempo,d,label='Distância percorrida (km)'); ax1.set_xlabel('Tempo (h)'); ax1.grid(True); ax1.set_yticks(np.linspace(-100,100,5)); #Plotando a aceleração em outro eixo ax2 = ax1.twinx(); #criando um eixo igual ax2.plot(tempo[1:-1],dvdt_m*kmh2toms2,label=r'Aceleração (m/s²)',lw=1,alpha=0.5,color='g'); ax2.set_ylabel('Aceleração (m/s²)',color='g') ax2.set_yticks(np.linspace(-0.4,0.4,5)) ax2.tick_params(axis='y', labelcolor='g') # Adicionando uma legenda na figura (Não é no eixo) # Documentação: https://matplotlib.org/3.1.1/api/_as_gen/matplotlib.pyplot.legend.html # Documentação do eixo: https://matplotlib.org/3.3.3/api/axes_api.html fig.legend(loc='lower center', #Posição da legenda ncol=3, #Colocando a legenda na horizontal bbox_to_anchor=ax1.get_position() #Criando um eixo artifical com o tamanho do eixo 1 ); fig.tight_layout(); #Ajuste fino
Atividade 3: Outras aplicações do Sympy
Nos tópicos anteriores vimos a aplicação do Sympy com derivadas e integrais. Contudo, o Sympy é um biblioteca muito completa, com ela podemos diversas operações simbólicas e mostrar todo o processo de resolução de forma detalhada através das saídas do IPython ou através do Latex.
Neste tópico vamos abordar algumas aplicações úteis na prática.
Exemplo 11: Simplificações
Com o Sympy é possível simplificar expressões matemáticas. Uma lista mais completa com vários métodos está disponível aqui. Porém, vamos mostrar alguns exemplos.
Simplify
Função que simplifica expressões matemáticas:
\[\sin^{2}{\left(x \right)} + \cos^{2}{\left(x \right)}=1\]x=sym.symbols('x') #Criando a expresão expr=sym.sin(x)**2+sym.cos(x)**2 #Mostrando a saída simplificada Eqn(f'{sym.latex(expr)}={sym.simplify(expr)}')
Expand
Podemos usar o expand expandir polinômios:
\[\left(a + b\right)^{2}=a^{2} + 2 a b + b^{2}\]a, b=sym.symbols('a b') #Criando a expresão expr=(a+b)**2 #Mostrando a saída expandida Eqn(f'{sym.latex(expr)}={sym.latex(sym.expand(expr))}')
Outro exemplo:
\[\left(a - b\right) \left(a + b\right)=a^{2} - b^{2}\]a, b=sym.symbols('a b') #Criando a expresão expr=(a+b)*(a-b) #Mostrando a saída simplificada Eqn(f'{sym.latex(expr)}={sym.latex(sym.expand(expr))}')
Factor
A função factor fatora um polinônimo em fatores inrredutíveis:
\[\vec{\gamma} a_{\alpha}^{2} + 4 \vec{\gamma} a_{\alpha} a_{\beta} + 4 \vec{\gamma} a_{\beta}^{2}=\vec{\gamma} \left(a_{\alpha} + 2 a_{\beta}\right)^{2}\]a1, a2, g = sym.symbols('a_{\\alpha} a_{\\beta} \\vec{\\gamma}') #Observe que podemos utilizar nomes do latex #Criando a expressão expr=a1**2*g + 4*a1*a2*g + 4*a2**2*g Eqn(f'{sym.latex(expr)}={sym.latex(sym.factor(expr))}')
Exemplo 12: Matrizes
\[\left[\begin{matrix}- 2 x - y\\- x + 2 y - z\\2 z\end{matrix}\right]\]# Multiplicação A*X\[\left[\begin{matrix}x + 3\\y + 5\\z + 7\end{matrix}\right]\]# Soma B+X\[\left[\begin{matrix}3 x\\5 y\\7 z\end{matrix}\right]\]# Multiplicação termo a termo B.multiply_elementwise(X)\[\left[\begin{matrix}- \frac{2}{5} & - \frac{1}{5} & - \frac{1}{10}\\- \frac{1}{5} & \frac{2}{5} & \frac{1}{5}\\0 & 0 & \frac{1}{2}\end{matrix}\right]\]# Inversa A.inv()\[-10\]# Determinante A.det()\[X=\left[\begin{matrix}x\\y\\z\end{matrix}\right]=\left[\begin{matrix}-2 & -1 & 0\\-1 & 2 & -1\\0 & 0 & 2\end{matrix}\right]^{-1}\left[\begin{matrix}3\\5\\7\end{matrix}\right]=\left[\begin{matrix}- \frac{29}{10}\\\frac{14}{5}\\\frac{7}{2}\end{matrix}\right]\]# Resolvendo o sistema linear Eqn(f'X={sym.latex(X)}={sym.latex(A)}^1{sym.latex(B)}={sym.latex(A.inv()*B)}')
Selecionando elementos:
\[\left[\begin{matrix}-2 & -1 & 0\end{matrix}\right]\]# Primeira linha A.row(0)\[\left[\begin{matrix}0\\-1\\2\end{matrix}\right]\]# Última coluna A.col(-1)\[-2\]#secionando o elemento [0,0] A[0,0]
Equações 13: Equações
Podemos utilizar o Sympy para resolver equações comuns ou equações diferenciais.
Atividade 4: Publicando seu Notebook
O formato nativo do Jupyter Notebook ainda não é aceito em muitos locais. Desta forma, sempre que for necessário publicar seu Notebook, seja para uma disciplina da escola ou universidade, ou simplesmente um site da Web é necessário converte-lo para um formato aceito.
Exemplo 14: Exportando Notebook estáticos
Basicamente existem duas formas de converter um notebook estático (Entenda Notebook estático como aquele sem a interação com o usuário). Através do menu do Jupyter, linha de comando (no terminal) ou através de código Python.
De acordo com a documentação você pode exportar o seu Notebook para:
- Apresentações de informações em formatos mais familiares como PDF
- Publicação do seu Notebook em artigos científicos utilizando o LaTeX
- Colaboração com outros que não são familiares com o formato de Notebooks
- Publicação para várias pessoas na web usando HTML
Você pode encontrar algumas opções de importação no Menu do Jupyter:
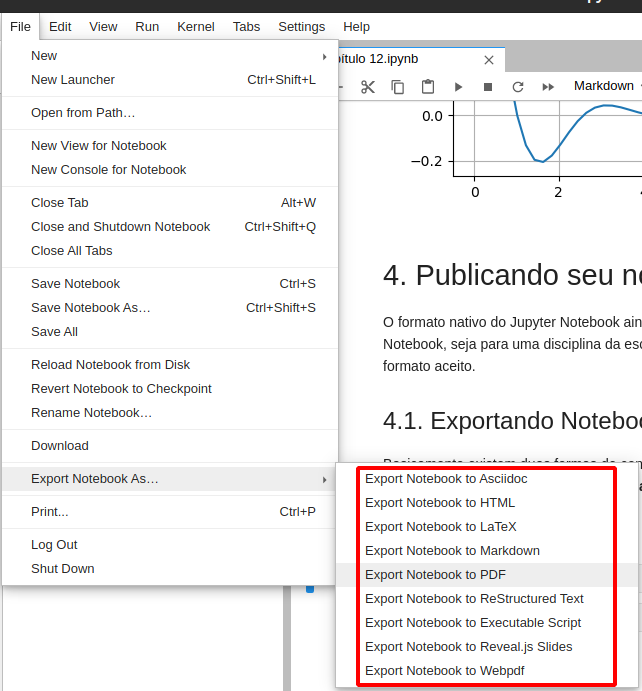
Observe que existem vários formatos de conversão, entretanto é bem provável que alguns deles não execute sem erros, pois ao clicar em cada um dessas opções o Jupyter rodar um script que depende de dependências externas. Abaixo tem-se uma tabela com os seguintes formatos que iremos abordar.
- Script
Converte o Notebook em um arquivo
.py. As células markdown são convertidas em comentários.
- HTML
Formato da Web é útil quando quer transformar seu notebook é uma página web ou em um post de um blog
- Markdown
Para converter o seu notebook para Markdown talvez seja necessário ter o Pandoc instalado. > Pandoc é um conversor de documentos universal que o Jupyter usar para converter o Notebook em formatos diversos.
- LaTeX
Assim como no Markdown, talvez seja necessário o uso do Pandoc para fazer a conversão para do Notebook para LaTeX.
O conversor de PDF do Jupyter converte o texto primeiro para o LaTeX para depois fazer a conversão para PDF utilizando uma distribuição como o Miktex ou TeX Live. Provavelmente se você tiver as dependeências citadas tudo funcionará perfeitamente.
- Reveal.js Slides
É possível converter o Notebook em slides. Iremos entrar em detalhe mais tarde.
Não existe fórmula mágica:
Nem sempre a conversão do Notebook irá funcionar sem erros. Muitas vezes será necessário outras dependências para fazer a conversão de alguns Notebooks. Por exemplo:
Para fazer conversão de arquivos que usam SVG é necessário ter o Inkscape instalado. Desta forma, sempre é importante observar o console de erro para verificar quais dependências estão faltando e instalá-las. Contudo, ao instalar as dependências citadas é bem provável que a conversão funcione na maioria dos casos.
Tarefa 2: Exporte seu notebook para pdf pelo menu do Jupyter.
Exemplo 15: Utilizando a linha de comando
Uma outra forma de compartilhar seu Notebook é através do comando nbconvert. A vantagem de utilizar a linha de comando é que é possível customizar a sua conversão. Por exemplo:
- Podemos remover o código ou células específicas
- Podemos adicionar citações na saída LaTeX ou PDF
- Exportar para templates personalizados
Na prática o Menu do Jupyter usa alguns presets do nbconvert, desta forma, se houver erros tanto no menu do Jupyter quanto no nbconvert é interessante que você leia a documentação:
Abaixo tem alguns exemplos do uso da linha de comando:
- Convertendo um notebook para Markdown:
jupyter nbconvert "cap11" --to markdown
- Convertendo um notebook para PDF e removendo os códigos:
jupyter nbconvert "cap11" --to pdf --TemplateExporter.exclude_input=True
- Convertendo um notebook para HTML usando um nome específico de saída:
jupyter nbconvert "cap11" --to html --output "post.html"
Exemplo 16: Templates
O nbconvert fornece alguns templates que podem ser alterados através de um parâmetro na linha de comando. Ao instalar o Anaconda não existem muito templates prontos, porém você pode criar ou customizar os já existentes.
Na versão 6 os templates estão disponíveis na pasta:
[Pasta do Anaconda]/share/jupyter/nbconvert/templates
O Templates são feitos com linguagem Jinja. Jinja é uma linguagem “server-side” que permite adicionar lógica dentro da construção de documentos (Semelhante ao PHP, Liquid, e outros).
A linguagem é relativamente simples, muito provavelmente ao observar os arquivos na pasta Templates você consiguirá interpretar algumas coisas. Entretanto, a linguagem Jinja não é o foco do curso, para isso será disponibilizado
Como este não é o foco do curso será disponibilizado o link da documentação de como adicionar suporte a novos templates:
Contudo nada impede de customizar os templates existentes. Por exemplo, podemos mudar o idioma para português adicionando a seguinte linha ao arquivo latex/base.tex.j2:
\usepackage[portuguese]{babel}
Para customizações mais avançadas você pode converter diretamente para o LaTeX.
Tarefa 3: Exporte seu arquivo para PDF e esconda o código.
Exemplo 17: Slides
É possível exportar o seu Notebook para o formato de Slides através da exportação para o RevealJS.
Para exemplificar o uso dos slides abra o arquivo slides.ipynb. Este arquivo foi configurado para apresentar na forma de Slides. Clique na engrenagem (Como mostra a Figura abaixo) e escolha o tipo de slide:
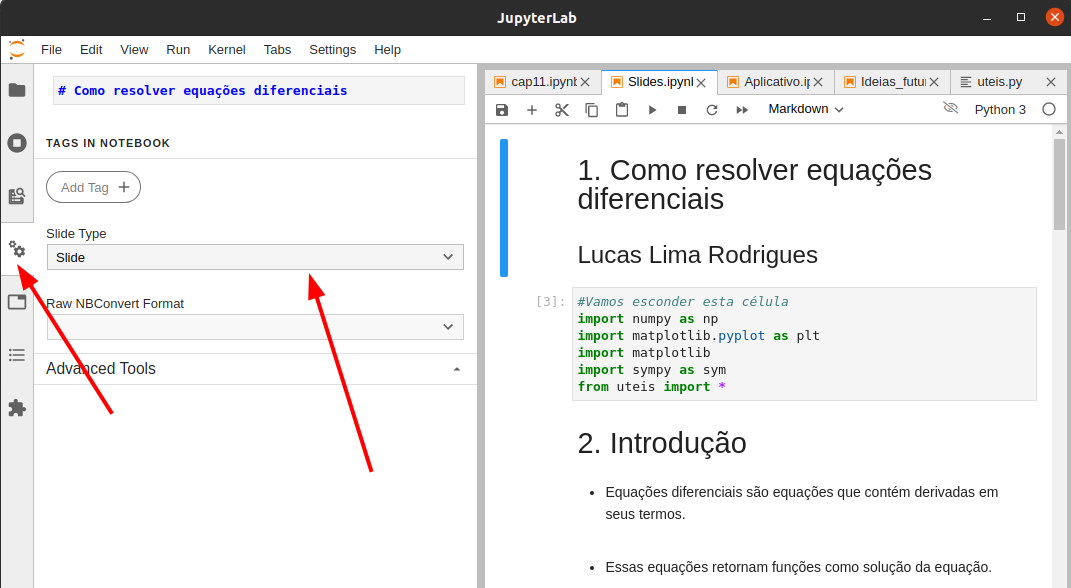
São basicamente 4 tipos de slides:
Slide$\rightarrow$ Início do slide (Ou de uma seção)Sub-slide$\rightarrow$ Continuação do slide (Aparece com uma animação para baixo)Fragment$\rightarrow$ Semelhante aoSub-slidesó que só aparece se o usuário apertar uma tecla.Hide$\rightarrow$ Esta célula não aparece no slideNotes$\rightarrow$ Não aparece para o público (Semelhante às notas do Power Point)
Para publicar e visualizar seus slides você deve recorrer ao terminal e executar o seguinte comando com o nbconvert:
jupyter nbconvert "Slides" --to slides --post serve --TemplateExporter.exclude_input=True
Desta forma você irá exportar o seu arquivo para html, esconder o código e executar um servidor para rodar as animações dos slides.
Exemplo 18: Exportando Notebooks para Web Apps
O nbconvert não permite Notebooks com interação com usuário. Para isso devemos utilizar outra biblioteca como o Voila. Voala permite transformar Notebooks em Web Aplicativos.
No nosso exemplo vamos adicionar mais um Slide ao nossos slides e configurá-lo como Slide dinâmico com Widgets.
O primeiro passo para utilizar o Voila é fechar o Anaconda e instalar o voila:
conda install -c conda-forge voila
ou
pip install voila
Feito isso, basta utilizar a linha de comando assim como fizemos para os outros casos do nbconvert:
voila App.ipynb
Com a extensão @jupyter-voila/jupyterlab-preview rodar um preview do Voilà diretamente da interface do Jupyter. Você pode instalá-la através do comando abaixo ou através da interface do Jupyter.
jupyter labextension install @jupyter-voila/jupyterlab-preview
Exemplo 19: Slides dinâmicos
É possível criar Slides com Widgets dinâmicos com o Voila. Para isso é necessário instalar outro pacote que adiciona o template do Reveal js. Feche o Anaconda e instale usando um dos comandos abaixo:
conda install -c conda-forge voila-reveal
ou
pip install voila-reveal
Agora é só abrir o arquivo App.ipynb e executar o comando comando:
voila "App.ipynb" --template=reveal
Exemplo 20: Publicando o seu App na Web
Existem diversos serviços na nuvem que permitem upar seu Notebook Dinâmico usando o Voila. A documentação do Voila cita 3:
- Binder $\rightarrow$ Um dos principais serviços utilizados para compartilhar notebooks
- Heroku $\rightarrow$ Serviço gratuito amplamente utilizado para Notebooks e Webapss
- Google App Engine $\rightarrow$ Serviço pago da Google
Mais detalhes podem ser encontrados no link abaixo:
Dica: Ao upa o seu notebook na Nuvem você pode compartilhar seus slides.