Capítulo 3: Módulos e pacotes

Atividade 1: Importando módulos

O python possui muitas funções e operadores que nativa da própria linguagem de programação como os operadores básicos (+,-,*,/), potenciação (**) impressão de valores (print(),.format()), e etc.

No entanto, há algumas funcionalidades que você irá precisar para produzir seu código, mas que não tem nativamente na linguagem Python, podemos então importar tais funcionalidades para o nosso trabalho como módulos.

Agora vejam a definição de módulo segundo um trecho da a própria documentação do Python:

Módulos são um conjunto de códigos como funções, classes, variáveis, etc. Se você estiver fazendo um programa e ele se tornar muito grande, difícil de ler e se situar nele, é uma boa prática dividi-lo em arquivos menores, para facilitar a manutenção. Também é preferível usar um arquivo separado para uma função que você escreveria em vários programas diferentes, para não copiar a definição de função em cada um deles.

Para permitir isso, o Python tem uma maneira de colocar as definições em um arquivo e então usá-las em um script ou em uma execução interativa do interpretador. Tal arquivo é chamado de módulo; definições de um módulo podem ser importadas para outros módulos, ou para o módulo principal.

Exemplo 1: Importando um módulo

Para o nosso primeiro exemplo vamos importar o módulo math, um módulo que estende o Python com algumas funcionalidades matemáticas.

Execute a célula abaixo:

import math # Nesta linha eu estou importando o módulo math

Feito isso, tente escrever o seguinte código e aperte Tab:

math.

Você verá todas as funções e constantes (instâncias) deste pacote, como mostra na Figura abaixo:

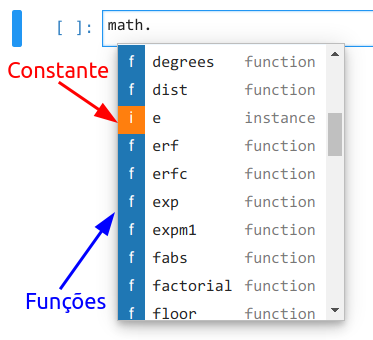
Tab Módulos

Agora apague a célula acima e vamos aprender a calcular a raiz quadrada. Para isso utilize a função sqrt() do módulo math.

num = int(input("Digite o número que quer calcular a raiz quadrada: "))
raiz = math.sqrt(num) # A função sqrt() do módulo 'math' calcula a raiz quadrada 
print("A raiz quadrada de {num} é {raiz}".format(num=num,raiz=raiz))

Digite o número que quer calcular a raiz quadrada: 4
A raiz quadrada de 4 é 2.0

Dica: Teste o exemplo acima com alguns valores, como 5, 4, 3, 2, etc.

Agora vamos arredondar o resultado da raiz utilizando a função ceil().

num = int(input("Digite o número que quer calcular a raiz quadrada: "))
raiz = math.sqrt(num) # A função sqrt() do módulo 'math' calcula a raiz quadrada 
arredondar = math.ceil(raiz) # A função ceil() arredonda para cima um determinado valor
print("A raiz quadrada (arredondada) de {num} é {raiz}".format(num=num,raiz=arredondar))

Digite o número que quer calcular a raiz quadrada: 5
A raiz quadrada (arredondada) de 5 é 3

Dica: Teste os exemplos acima com alguns valores, como 5, 4, 3, 2, etc.

Vamos praticar com uma constante. Procure a constante pi e execute:

math.pi
3.141592653589793

Agora vamos criar um programa capaz de calcular o seno de um ângulo dado em graus:

ang_graus = int(input("Digite um ângulo (Em graus): "))
ang_rad = ang_graus*math.pi/180 #Observe que estamos utilizando a constante pi
seno = math.sin(ang_rad) # A função sin() calcula o seno de um ângulo
print("O seno de {ang_graus}° é {seno:.2g}".format(ang_graus=ang_graus,seno=seno))

Digite um ângulo (Em graus): 60
O seno de 60° é 0.87

Dica: Teste o exemplo acima com os ângulos 0, 30, 45, 60 e 90.

Tarefa: Crie um código que aceite um ângulo em graus como entrada, e imprima na tela o seu correspondente em radianos, o seu seno, cosseno e tangente.

Observação: Utilize a função radians() para fazer a conversão de graus para radianos diretamente.

Dica: Utilize as funções sin(), cos(), tan() para calcular o seno cosseno e tangente.

A saída do programa deve ser parecida com isso:

Digite o ângulo em graus:  45
O ângulo 0.79 rad, tem o seno 0.71, cosseno 0.71 e tangente 1

Dica: Teste o exemplo acima com os ângulos 0, 30, 45, 60 e 90.

Exemplo 2: Documentação do `math`

Praticamente todo módulo ou pacote do Python tem uma documentação disponível na internet. O módulo math é um módulo built-in, ou seja, ele é um módulo que já vem junto com o Python. Para estes módulos podemos olhar a própria documentação do Python. Essa documentação está disponível no menu Help>Python Reference ou no próprio site do python, na parte de Docs.

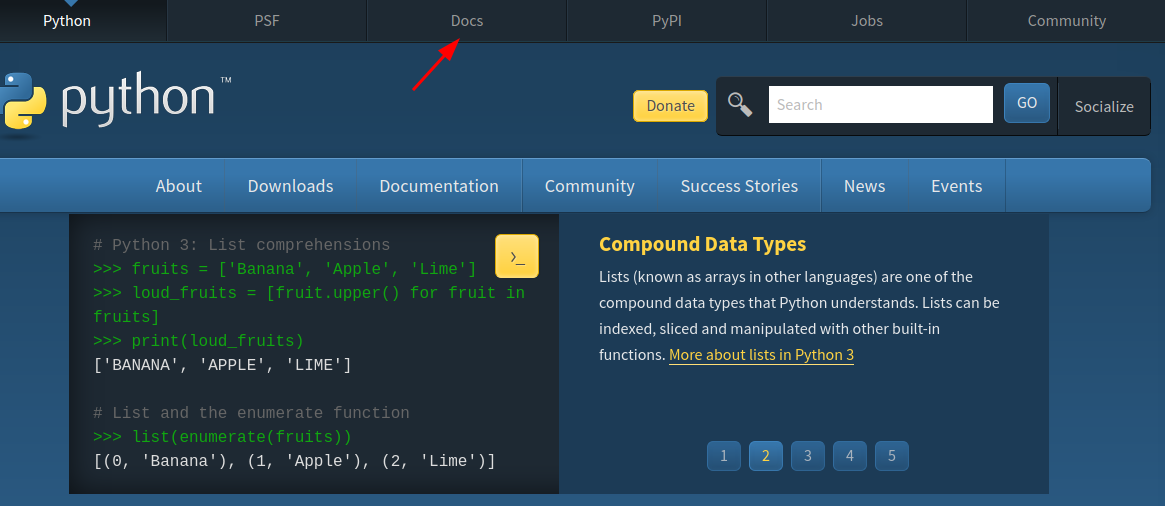
Site do Python

No caso do módulo de matemática, podemos utilizar o seguinte módulo direto:

https://docs.python.org/3/library/math.html

Lá podemos encontrar explicações detalhadas de todas as funções e constantes do módulo math.

Tarefa 1: Buscando na documentação do módulo math, crie um programa capaz de calcular as seguintes expressões:

$e^x$
$x!$
$\log_{10}(x+1)$
$(\pi+e)^x$

O usuário deve colocar como entrada o valor de $x$.

Observação: Teste usar a função pow() no lugar do operador **.

A saída deve ser parecida com essa:

Digite o valor de x:  1
e^1=2.72
1!=1
log10(1+1)!=0.30
(pi+e)^1!=5.86

Tarefa 2: Crie um programa capaz de calcular a hipotenusa de um retângulo utilizando uma função do módulo math.

Sugestão de saída:

Digite o primeiro cateto: 3
Digite o segundo cateto: 4
A hipotenusa é 5

Exemplo 3: `from` … `import` …

É muito chato toda vez que for utilizar alguma funcionalidade da função math, ter que escrever math. no início. Através da sintaxe:

from [módulo] import [função1], [função2], [constante1], [etc]

Podemos incluir somente as funções e constantes que desejamos trabalhar e eliminamos a necessidade de utilizar math. no início. Veja o exemplo:

from math import pi
pi
3.141592653589793

Vejamos um exemplo de como calcular o fatorial:

# Utilizando import
import math 
numero = int(input("Digite um valor: "))
fat = math.factorial(numero)
print("O fatorial de {} é {}.".format(numero, fat))

Percebemos agora, a maneira mais simples de importar um módulo, que é simplesmente digitando import e o nome do módulo logo em seguida. Na hora de chamar a função factorialprecisamos especificar que ela pertence ao módulo em questão, por isso a chamamos com math.factorial().

Agora suponha que iremos usar apenas a função factorial, sem usar as outras funções do módulo de matemática, a outra forma de faze-lo é:

# Utilizando from import
from math import factorial
numero = int(input("Digite um valor: "))
fat = factorial(numero)
print("O fatorial de {} é {}.".format(numero, fat))

Tarefa: Refaça a tarefa abaixo importando todas as funções necessárias utilizando a notação from import

Crie um código que aceite um ângulo em graus como entrada, e imprima na tela o seu correspondente em radianos, o seu seno, cosseno e tangente.

Exemplo 4: `from` … `import` *

Caso não soubermos as funções que iremos utilizar, ou se iremos utilizar muitas funções de um determinado módulo, podemos importar todas as funções deste módulo utilizando a notação:

from [módulo] import *

Veja o exemplo abaixo:

from math import *
ang_graus = int(input("Digite um ângulo (Em graus): "))
ang_rad = ang_graus*pi/180 #Observe que estamos utilizando a constante pi
print("O seno de {}° é {:.2g}".format(ang_graus,sin(ang_rad)))

Digite um ângulo (Em graus): 60
O seno de 60° é 0.87

import * é prático! Mas tome cuidado!

Segue alguns motivos para não usar o import *:

Seu código não fica legível
Não fica implícito no código da onde vem aquela função
Caso um ou mais módulos tenham duas funções com o mesmo nome, você não tem como escolher, sempre será selecionada a última função importada!
Bugs inesperados
Etc

Isso não quer dizer que usar o import * é sempre ruim. Ele pode ser prático em códigos pequenos, ou em módulos que você já conhece bem e que você saiba o que está fazendo.

Para mais detalhes clique aqui.

Exemplo 5: Outros módulos built-in

Além do módulo math, existem outros módulos built-in e você pode encontrá-los na documentação do Python, em Library reference (A página tem o título Python Library Standard )

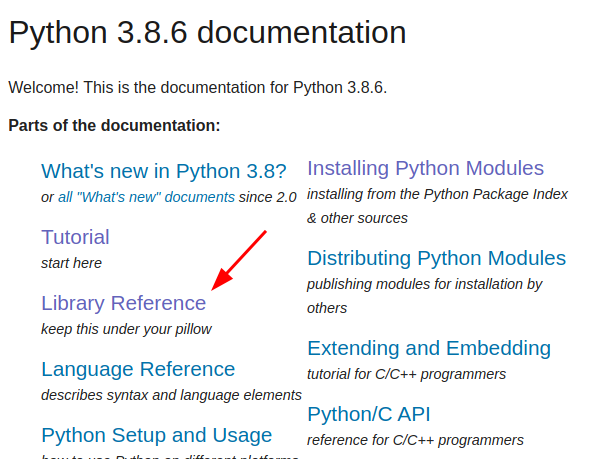
Bibliotecas Built-in do Python

Esta página mostra diversos módulos em formas de categorias.

Para continuarmos os nossos exercícios vamos utilizar uma outro módulo de matemática, o módulo random. Ele está na seção Numeric and Mathematical Modules. Vamos ver um exemplo com a função random():

from random import random # A função random() gera um float pseudo aleatório de 0.0 <= x < 1.0
from math import floor # A função ceil() arredonda para baixo

aleatorio=floor(10*random()) # Gera um número pseudo aleatório de 0 a 9
aleatorio

Observe que nesse exemplo para conseguir esse efeito combinamos duas funções de módulos diferentes.

Tarefa 1: Olhando a documentação do módulo random refaça o exemplo sem utilizar o módulo math.

Tarefa 2: Lendo a documentação indique quais módulos são mais adequados para:

Trabalhar com o tempo (Horas, dias, semanas)
Trabalhar com arquivos de audio do tipo WAV
Criar programas com interface gráfica (GUI)
Trabalhar com frações

Exemplo 6: Renomeando módulos

Uma outra forma de importar módulos é renomeando-o. Observe novamente o exemplo do fatorial:

import math as m
numero = int(input("Digite um valor: "))
fat = m.factorial(numero)
print("O fatorial de {} é {}.".format(numero, fat))

Digite um valor: 5
O fatorial de 5 é 120.

Observe que a sintaxe import math as m tornou o mesmo módulo disponível agora por um nome diferente, no caso, mat. Dessa forma, podemos chamar uma função do módulo como m.função, como mostrado acima. Essa funcionalidade é particularmente útil quando o nome do módulo é grande e a tarefa de escreve-lo diversas vezes torna-se chata, como é mostrado abaixo:

import matplotlib.pyplot as plt # Submódulo para plotar gráficos

Sempre prefira essa notação de import [nome_do_pacote] as [novo_nome_do_pacote]ao invés de apenas import , pois desta forma você deixa o código legível e evita a tarefa chata de ter que escrever o nome completo do módulo toda vez que vai utilizar uma funcionalidade do módulo.

Tarefa: Considere o código abaixo, substitua o from math import * por ìmport math as m:

from math import *
ang_graus = int(input("Digite um ângulo (Em graus): "))
ang_rad = ang_graus*pi/180 #Observe que estamos utilizando a constante pi
print("O seno de {}° é {:.2g}".format(ang_graus,sin(ang_rad)))

Atividade 2: Pacotes do Anaconda

Como dito anteriormente, podemos ver os módulos como se fossem caixas com diversas funções úteis dentro, e que podemos acessa-las com um import.

classDiagram
	class Math{
		<<Módulo>>
		pi
		e
		inf
		etc
		ceil(x)
		comb(n,k)
		copysign(x,y)
		etc()
	}

Figura 1: Representação do módulo Math.

No python, também há o conceito de Pacote. Podemos ver os pacotes como módulos que contém outros módulos separados por temática. Na imagem abaixo temos o pacote Game. Dentro deste pacote existem outros módulos.

classDiagram
	  Game .. Som
	  Game .. Imagem
	  Game .. Fase
      class Game{
		<<Pacote>>
      }
      class Som{
      <<Sub-Módulo>>
      	volumeEfeito
      	volumeMusica
      	reproduzirEfeito()
      	reproduzirMusica()
      	mudarVolume()
      }
      class Imagem{
      <<Sub-Módulo>>
      	qualidade
      	filtros
      	mudarQualidade()
      	mudarFiltros()
      }
      class Fase{
      	<<Sub-Módulo>>
      	mundo
      	numero
      	chefe
      	entrar()
      	derrotarChefe()
      }

Figura 2: Conceito de pacote.

O nosso pacote fictício agora possui vários sub-módulos, cada um deles com diversas funções diferentes e de modo mais organizado na visão do programador.

Muitos dos pacotes utilizados pela comunidade Python não vem por padrão na linguagem. Por sorte o Anaconda trás diversos pacotes úteis para o programador Python. Desta forma não precisamos nos preocupar em instalar muitos pacotes utilizados na comunidade Python. Podemos citar alguns exemplos de pacotes que vem junto com o Anaconda:

Numpy - Gerenciamento de arrays e matrizes
Matplotlib - Gráficos e plotagens
Scipy - Computação científica
Sympy - Variáveis simbólicas
Seaborn - Visualização de dados com estatística
Pandas - Análise de dados
OpenCV - Processamento de imagens
TensorFlow - Machine learning
Pillow - Visualização e filtragem de imagens
Orange - Análise de dados

Pode ser que na sua máquina estes pacotes não estejam instalados. Entretanto podemos instalá-los utilizando o terminal e utilizando o comando:

conda install [pacote]

O conda é o gerenciador de pacotes do Anaconda. Através desse comando podemos instalar, pesquisar e desinstalar pacotes. Abaixo segue alguns comandos que podemos utilizar no gerenciador de pacotes do Anaconda.

Comando	Função
`install [pacote]`	Instala um pacote
`--help`	Ajuda
`uninstall [pacote]`	Remove um pacote
`search [palavra]`	Procura por um determinado pacote baseado em uma palavra
update	Faz o update de todos os pacotes do Anaconda

Exemplo 1: Gerenciador de pacote `conda`

Tarefa: Utilizando o comando conda search tente procurar pelos seguintes pacotes:

Orange
OpenCV
Pillow

Agora instale o pacote Orange. Utilize a sequencia de comandos abaixo:

conda search orange
conda install orange3

Feche a abra o Anaconda.

Verá que agora é possível abrir o Orange no Anaconda Navigator.

Finalmente, desinstale o Orange.

Exemplo 2: Aplicação de um pacote

Para entender melhor o conceito de pacote vamos utilizar o exemplo de uma trajetória de um projetil.

O pacote sympy permite trabalhar com variáveis simbólicas. Variáveis simbólicas são variáveis que armazenam uma incógnita, como por exemplo $t$, $x$, $y$.

Observação: A documentação deste pacote pode ser encontrada no menu Help > Sympy Reference. Alternativamente você pode clicar aqui.

A documentação dos módulos disponíveis nesse pacote pode ser encontrada clicando aqui.

Módulos do Sympy

Observe que neste pacote existem muitos submódulos, que contém muitas classes e funções. Para facilitar a nossa vida, segue o diagrama abaixo que apresenta apenas funções importantes para este exemplo:

classDiagram
	sympy .. plotting
	class sympy{
		pi
		symbols()
		cos()
		sin()
	}
	class plotting{
		plot()
		plot_parametric()
	}

Figura 3: Funções do pacote sympy utilizadas nessa atividade.

Agora, considere que a trajetória de um projétil lancada na superfície da terra é governada pela seguinte função: $f(x)=-5x^2+20x$ Antes de tudo é necessário importar sympy.

import sympy

Observação: Caso apareça um erro ao importar sympy provavelmente o pacote não está instalado na sua máquina. Use o comando:
conda install sympy

Depois podemos criar a variável simbólica de $x$ usando a função symbols():

x = sympy.symbols('x') 
x

$x$

Feito isso podemos escrever a trajetória do projétil:

f=-5*x**2+20*x
f
$-5x^2+20x$

Se quisermos plotar a trajetória desse projétil devemos recorrer ao submódulo plotting que pertence a pacote sympy. Observe na Figura 3 que o submódulo está em uma hierarquia abaixo de sympy, então devemos utilizar a notação abaixo:

import [nome_do_pacote].[submodulo]

Importando o submódulo plotting:

import sympy.plotting #importando o submódulo plotting do pacote sympy

Agora podemos plotar a trajetória utilizando a função plot() neste submódulo:

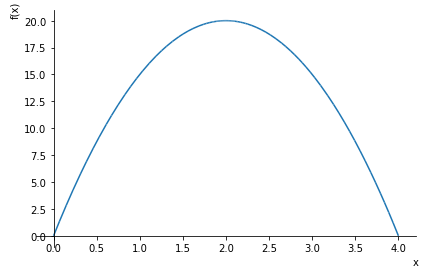
sympy.plotting.plot(f,(x,0,4))

Trajetória do projetil

Observe que usamos a expressão (x,0,4) para limitarmos a plotagem entre $0$ e $4$. Se tirarmos essa opção ele vai definir o intervalo de $-10$ à $10$.

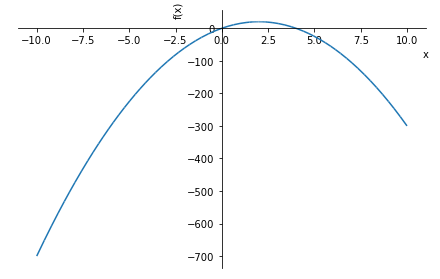
sympy.plotting.plot(f)

Trajetória do projétil sem limites

O que é fisicamente impossível, pois estamos considerando que o solo está situado em $x=0$.

Observe que para utilizar a função plot() tivemos que escrever o nome do submódulo inteiro. Para evitar essa tarefa chata podemos recorrer às sintaxes from … import … ou import … as … . Veja o mesmo exemplo acima reescrito:

from sympy import symbols
import sympy.plotting as plt

x = symbols('x')
f = -5*x**2+20*x
plt.plot(f,(x,0,4))

Trajetória do projetil

A notação from … import … também funciona com submódulos:

from sympy import symbols
from sympy import plotting

x = symbols('x')
f = -5*x**2+20*x
plotting.plot(f,(x,0,4))

Trajetória do projetil

E ainda, podemos customizar o nosso gráfico adicionando parâmetros na função plot(), que estão disponíveis na documentação. Alguns destes parâmetros estão disponíveis na tabela abaixo:

Função
title	Adiciona um título
xlabel	Adiciona um título para o eixo x
ylabel	Adiciona um título para o eixo y
xlim	limita o intervalo do eixo x
ylim	limita o intervalo do eixo y
line_color	Mudar a cor do gráfico (Utilize o nome das cores em inglês)

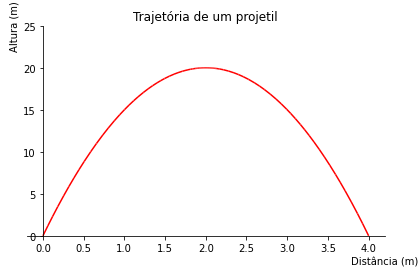
from sympy import symbols
from sympy.plotting import plot

x = symbols('x')
f = -5*x**2+20*x
plot(f,(x,0,4),
  ylim=(0,25),
  xlabel="Distância (m)",
  ylabel="Altura (m)",
  title="Trajetória de um projetil",
  line_color = 'Red'
 )

Trajetoria do projetil customizada

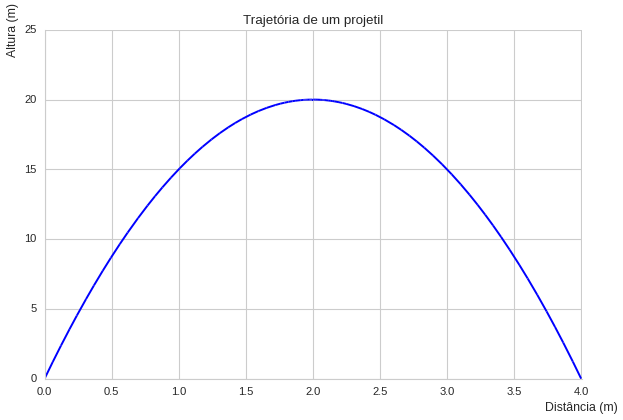
Podemos customizar um pouco mais o nosso gráfico utilizando o submódulo style do pacote matplotlib, através da função use().

from sympy import symbols
from sympy.plotting import plot
from matplotlib import style
style.use('seaborn-whitegrid')

x = symbols('x')
f = -5*x**2+20*x
plot(f,(x,0,4),
  ylim=(0,25),
  xlim=(0,4.005), #Adicionando um pouco mais de espaço para corrigir a grid
  xlabel="Distância (m)",
  ylabel="Altura (m)",
  title="Trajetória de um projetil"
 )

Para encontrar mais estilos você pode clicar aqui, ou através da documentação do pacote.

Observação: Iremos ver o pacote matplotlib com mais detalhes futuramente.

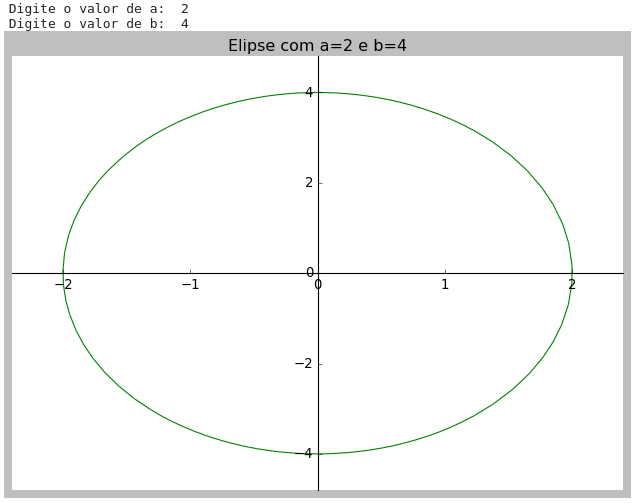
Tarefa: A equação paramétrica de uma elipse é dada por: $\begin{cases} x(\theta)=a\cos(\theta)\\ y(\theta)=b\sin(\theta) \end{cases}$ Construa um programa capaz de gerar uma elipse utilizando a função plot_parametric(), seguinte as seguintes premissas:

O programa deve ter como entrada $a$ e $b$;
O título do gráfico deve ter os raios $a$ e $b$;
Os limites dos eixos x e y devem ser $\pm1,2a$ e $\pm1,2b$, respectivamente;
Use o estilo classic;
O gráfico deve ter a cor verde.

Dicas:

Use ctrl+F na documentação para encontrar esta função.

Todas as funções que você precisa está na Figura 3.

A saída do seu gráfico deve ser parecida com:

Elipse

Atividade 3: Pacotes externos

Parte 1: Python Package Index (PyPI)

Existem outros gerenciadores de pacotes além do conda. O Python Package Index (PyPI), ou simplesmente pip, é o gerenciador padrão do Python, e muitas vezes só podemos encontrar um pacote neste gerenciador. Você pode encontrar um link do site oficial do pip no próprio site do Python.

Como encontrar o pip

Segundo este mesmo site no momento em que este roteiro está sendo escrito existem 267182 pacotes disponíveis para instalar através desse gerenciador.

Você pode encontrar uma pequena descrição do pacote ao buscar dentro desta plataforma.

Geralmente os pacotes têm seu código fonte disponível no Github, portanto se no site pypi não tiver muita informação desse pacote, procure-o no Github, com uma simples pesquisa no Google:

Imagens do Pyperclip

Observação: Inclusive este site está hospedado no Github.

Outro site muito relevante para encontrar documentação de pacotes em python é o Read the Docs, um site de documentação.

Read the Docs

Por exemplo, o própria documentação do JupyterLab está hospedada lá:

https://jupyterlab.readthedocs.io/en/latest/

A sintaxe de comando do pip é muito parecida com a do conda:

Comando	Função
`install [pacote]`	Instala um pacote
`--help`	Ajuda
`uninstall [pacote]`	Remove um pacote
`search [palavra]`	Procura por um determinado pacote baseado em uma palavra
update	Faz o update de todos os pacotes do Anaconda

Mais comandos podem ser vistos aqui.

Exemplo 1: Instalando um pacote

Para exemplificar o uso pip vamos instalar o pacote pyperclip:

Github: https://github.com/asweigart/pyperclip
Read the docs: https://pyperclip.readthedocs.io/en/latest/
Pypi: https://pypi.org/project/pyperclip/

Tarefa 1: Instale o pacote pyperclip (Entre no Pypi e copie o link

Exemplo 2: Exemplo de uso de um módulo

O módulo pyperclip é usado para trabalhar com os comandos copiar (Ctrl+C) e colar (Ctrl+V) do computador. Nele, há duas funções principais:

Função	Comando
copy()	Copia o conteúdo
paste()	Cola o conteúdo

classDiagram
	class pyperclip{
		copy()
		paste()
	}

import pyperclip as ppc

item1 = input("Digite o nome do item 1: ")
item2 = input("Digite o nome do item 2: ")
item3 = input("Digite o nome do item 3: ")
qt1 = int(input("Digite a quantidade do item 1: "))
qt2 = int(input("Digite a quantidade do item 2: "))
qt3 = int(input("Digite a quantidade do item 3: "))
i1 = "Item 1: " + item1
i2 = "Item 2: " + item2
i3 = "Item 3: " + item3


print("{:_^50}".format('Lista de estoque'))
print("{:-<45}{}".format("Item","Quant"))
print("{item:-<47}{quant:03d}".format(item=i1,quant=qt1))
print("{item:-<47}{quant:03d}".format(item=i2,quant=qt2))
print("{item:-<47}{quant:03d}".format(item=i3,quant=qt3))

lista = "{:_^50}\n".format('Lista de estoque')  + "{:-<45}{}\n".format("Item","Quant") + "{item:-<47}{quant:03d}\n".format(item=i1,quant=qt1)+"{item:-<47}{quant:03d}\n".format(item=i2,quant=qt2) + "{item:-<47}{quant:03d}\n".format(item=i3,quant=qt3)

ppc.copy(lista)

Digite o nome do item 1: Arroz
Digite o nome do item 2: Feijão
Digite o nome do item 3: Leite
Digite a quantidade do item 1: 4
Digite a quantidade do item 2: 1
Digite a quantidade do item 3: 6
______Lista de estoque______
Item——————————————————–Quant
Item 1: Arroz———————————-004
Item 2: Feijão———————————001
Item 3: Leite———————————-006

Tarefa: Substitua o último print() pelo seu Ctrl+C como saída de dados do seguinte código. Cole o resultado como uma célula Raw (OBS: Não é Markdown).

Dica: No modo de comando utilize a tecla R.

print("Este programa resolve uma equação de segundo grau do tipo ax²+bx+c=0")
a=int(input("Digite o valor de a: "))
b=int(input("Digite o valor de b: "))
c=int(input("Digite o valor de c: "))
delta=b**2-4*a*c
x1=(-b+delta**(1/2))/(2*a)
x2=(-b-delta**(1/2))/(2*a)
print("As soluções da equação {:f}x²+{:f}x+{:f}=0 são: x1={:g} e x2={:g}".format(a,b,c,x1,x2))

Parte 2: Exemplos de módulos e pacotes

No exemplo anterior utilizamos o pacote pyperclip, ele é um pacote útil para quem quer trabalhar com programas de interface que precisam de alguma forma trabalhar com a área de transferência.

Na área de Engenharia Elétrica existem uma infinidade de pacotes úteis que podem ser instalados através do pip (ou conda) ou seguindo as instruções no github.

Observação: Estou dando dicas de pacotes da Engenharia Elétrica, porque é a área que eu trabalho.

Agora vamos mostrar dois exemplos.

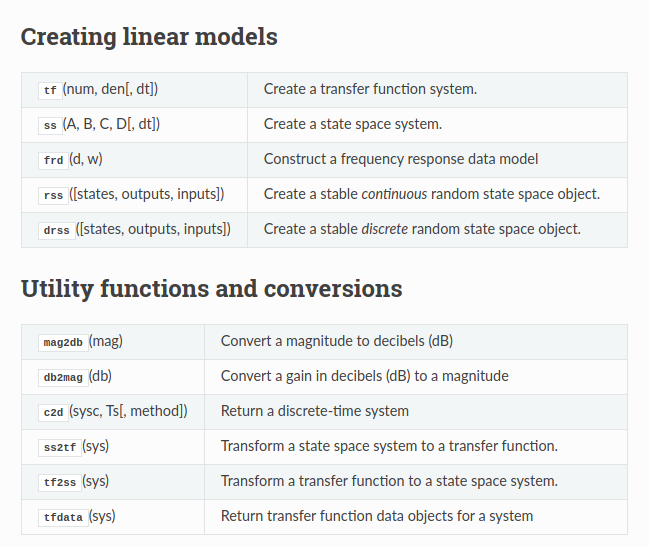
Exemplo 1: Python-control

Python Control Systems Library

Área: Engenharia Elétrica / Engenharia de controle e automação

Descrição: Permite a análise e operação de sistemas de controle.

Documentação: http://python-control.readthedocs.org/

Repositório (Github): https://github.com/python-control/python-control

Instalação (PyPI): https://pypi.org/project/control/

conda install -c conda-forge control slycot #Método recomendado

pip install slycot   # optional; see below
pip install control

Exemplo relevante:

https://github.com/python-control/python-control/blob/master/examples/bode-and-nyquist-plots.ipynb

Foto relevante:

Controle Linear

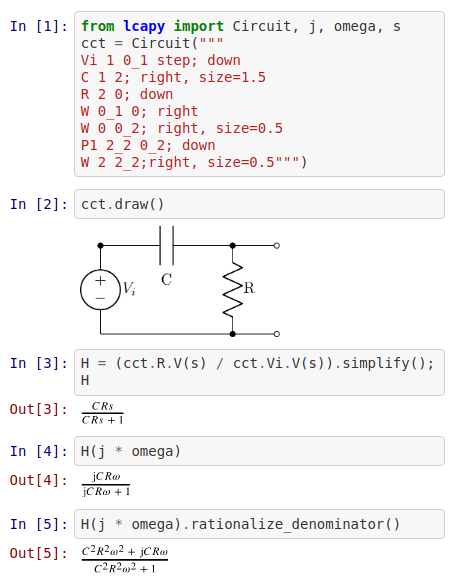
Exemplo 2: Lcapy

Linear Circuit Analysis

Área: Engenharia Elétrica

Descrição:

Lcapy é um pacote para análise de circuitos lineares.
Usa o SymPy para a análise simbólica.
Permite o desenho de alguns esquemáticos utilizando código Python.

Documentação: http://lcapy.elec.canterbury.ac.nz/

Repositório (Github): https://github.com/mph-/lcapy

Instalação (PyPI): https://pypi.org/project/lcapy/

pip install lcapy

Exemplo relevante:

https://github.com/mph-/lcapy/blob/master/doc/examples/notebooks/superposition1.ipynb

Foto relevante:

Exemplo do lcapy

Exemplo 3: Outros pacotes

Além dos pacotes citados nos Exemplos 1 e 2, existem muitos outros. Segue o nome de alguns:

pysimCoder $\rightarrow$ Editor parecido com o Simulink - Apenas Linux (Experimental)
PySpice $\rightarrow$ Simulador de circuitos
SchemDraw $\rightarrow$ Desenho de circuitos
py-dss-interface $\rightarrow$ Interface do Python com o OpenDSS (Não precisa instalar o OpenDSS) - Apenas Windows

Observação: Tomem cuidado ao instalar pacotes desatualizados, pois podem quebrar o seu ambiente Python. Sempre olhem as dependências antes de instalar o pacote.

Tarefa: Faça um resumo do Pacote graphviz. Siga o formato dos exemplos 1 e 2.

Para adicionar a foto utilize a sintaxe de foto do Markdown:

![Nome da foto](Caminho relativo da foto)
<!-- Exemplo -->
![Foto do blockdiag](imgs/blockdiag.png)

Para adicionar um link utilize a seguinte sintaxe:

[Nome do link](Caminho relativo da foto)
<!-- Exemplo -->
[Nome do link](http://www.blackdiag.com)

Se o link for uma URL basta copiar a URL.

Atividade 4: Para casa

Exercício 1: Média da turma

Crie um código que receba as notas do bimestre de 4 alunos conforme a tabela abaixo, compute a média e arredonde pra cima. Você deverá usar o módulo Math e consultar a documentação para entender a função que arredonda e usa-la no seu programa. O código deverá imprimir na tela a média final de cada um e o quanto cada aluno ganhou de nota no arredondamento.

Aluno	N1	N2	N3	N4
Pedrinho	7.00	8.75	8.3	5.6
Joãozinho	7.00	7.00	8.1	9.00
Juninho	6.40	7.50	8.45	9.00

Exercício 2: Plotando um gráfico

Crie um programa capaz de plotar uma onda seinodal no formato: $y(t)=Acos(\omega t+\delta)$ onde $A$ é a amplitude, $\delta$ é a fase da onda e $\omega=2\pi f$ é a frequência da onda.

O usuário deve entrar com $A$, $\delta$ e $f$.

Considere as seguintes premissas:

O título do gráfico deve ter todos os parâmetros da onda;
Os limites do eixo y deve ser $\pm1,2A$;
O limite do eixo x deve ser de $2$ segundos;
Use o estilo ggplot;
O gráfico deve ter a cor preta;
A variável $t$ deve ser simbólica;
Para a plotagem utilize função plot() do pacote sympy.

Veja o exemplo de saída:

Exemplo de saída

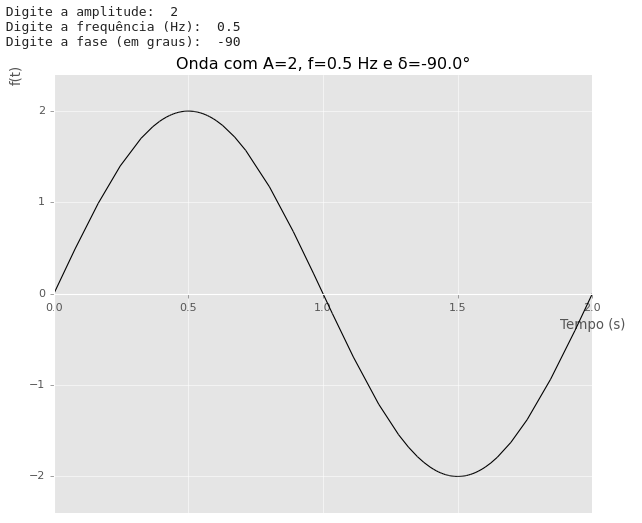
Exercício 3: Descobrindo pacotes

Pesquise na internet um pacote de Python que seja útil na sua área e faça um resumo desse pacote. Siga o formato dos exemplos da Atividade 3, parte 2.

Atividade 1: Importando módulos

Exemplo 1: Importando um módulo

Exemplo 2: Documentação do math

Exemplo 3: from … import …

Exemplo 4: from … import *

Exemplo 5: Outros módulos built-in

Exemplo 6: Renomeando módulos

Atividade 2: Pacotes do Anaconda

Exemplo 1: Gerenciador de pacote conda

Exemplo 2: Aplicação de um pacote

Atividade 3: Pacotes externos

Parte 1: Python Package Index (PyPI)

Exemplo 1: Instalando um pacote

Exemplo 2: Exemplo de uso de um módulo

Parte 2: Exemplos de módulos e pacotes

Exemplo 1: Python-control

Exemplo 2: Lcapy

Exemplo 3: Outros pacotes

Atividade 4: Para casa

Exercício 1: Média da turma

Exercício 2: Plotando um gráfico

Exercício 3: Descobrindo pacotes

Exemplo 2: Documentação do `math`

Exemplo 3: `from` … `import` …

Exemplo 4: `from` … `import` *

Exemplo 1: Gerenciador de pacote `conda`