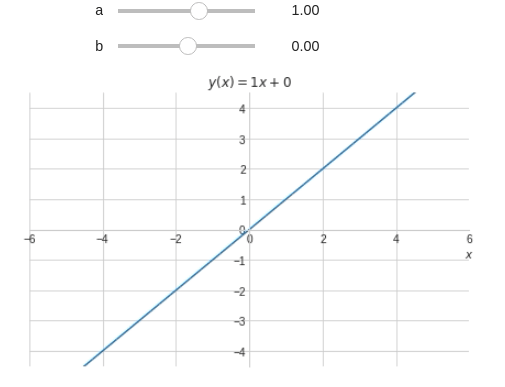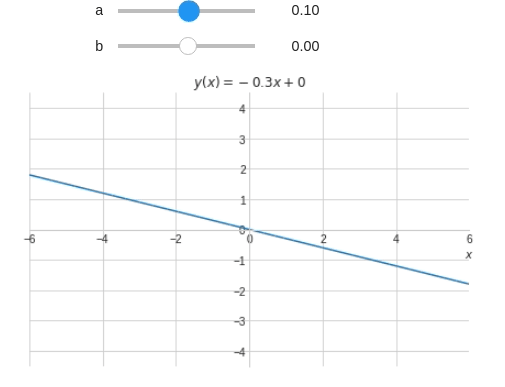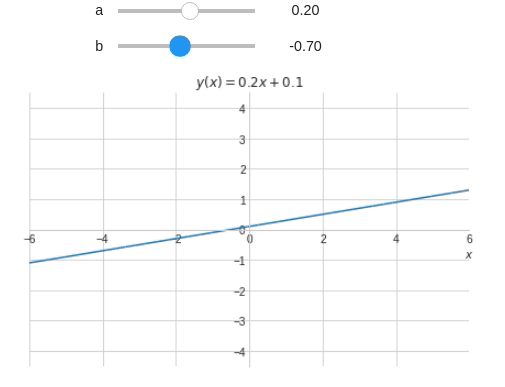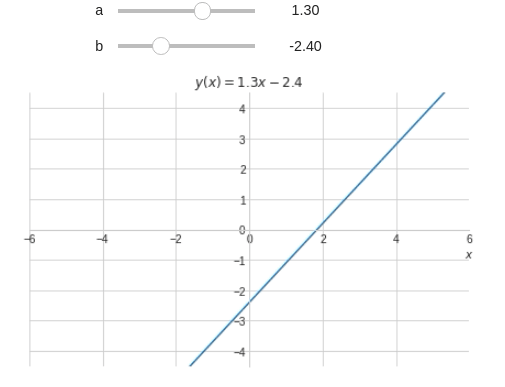Capítulo 6: Widgets

Atividade 1: Introdução aos Widgets

Até o momento vimos como entrada de dados a função input(). Contudo existem outras formas de entrada mais elegantes, como através do uso de pacotes e extensões do IPython.

O IPython é o backend do Jupyter e ele traz suporte a diversos itens de iteratividade que pode ser adicionados através de pacotes e extensões para o Jupyter. Um desses itens são os Widgets, que adiciona o suporte de entrada de dados de forma interativa.

Exemplo 1: Adicionando suporte à Widgets

Para adicionar suporte ao Widgets vamos recorrer ao pacote ipywidgets, cuja a documentação é apresentada em:

https://ipywidgets.readthedocs.io/

Para apresentar os widgets vamos começar adicionando um IntSlider().

import ipywidgets as widget #Importando o pacote com o apelido de widgets
widget.IntSlider() #Inicializando um IntSlider

IntSlider(value=0)

Contudo, ao executar esse código irá aparecer apenas um texto. Desta forma, a inclusão do pacote no código não é suficiente para adicionar o suporte a Widgets. Vamos resolver isso instando os Jupyter Widgets:

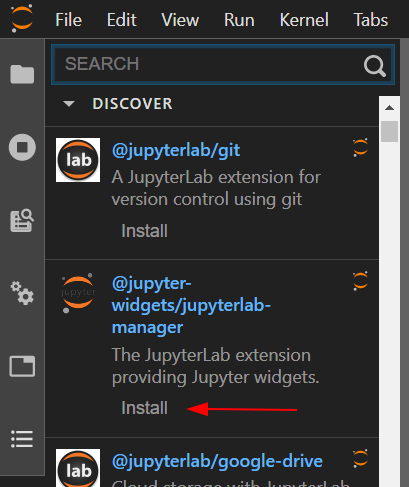
Observação: A instalação do Jupyter foi passada como tarefa para casa do capítulo 4. Se ainda não instalou, instale agora. Pode ser que demore um pouco a instalação.

Após a instalação execute o código novamente:

import ipywidgets as widget #Importando o pacote com o apelido de widgets
widget.IntSlider() #Inicializando um IntSlider

Verá que irá aparecer um Slider de inteiro.

Alternativamente, podemos mostrar sliders através da função display(), do módulo IPython.display:

from ipywidgets import IntSlider #Importando a função IntSlider
from IPython.display import display #Importando a função display

slider=IntSlider() #Inicializando o IntSlider
display(slider) #Mostra o slider

Provavelmente não será necessário importar a função display, pois ela já é carregada no Jupyter. Desta forma o código acima simplifica em:

from ipywidgets import IntSlider #Importando a função IntSlider

slider=IntSlider() #Inicializando o IntSlider
display(slider) #Mostra o slider

Observação: Reinicie o Kernel e teste.

Tarefa 1: Além do IntSlider existe uma extensa lista de Widgets que podem ser vista. Tente inicializar e mostrar os seguintes Widgets:

• Text
• Checkbox
• FloatSlider

Exemplo 2: Customizando os Widgets

De forma similar aos gráficos que aprendemos a plotar no capítulo anterior, os Widgets também são customizáveis.

Todas as opções de customizações de todos os tipos de sliders podem ser vistos na documentação. Porém, abaixo segue o exemplo com algumas opções de alguns Widgets que utilizaremos neste capítulo. Tentem executar todos os códigos:

• IntSlider retorna inteiros:

widget.IntSlider(
    value=5, # Valor inicial
       min=0, # Valor mínimo
       max=10, # Valor máximo
       step=1, # Passo
       description='Número:' #Descrição
   )

Número:

• FloatSlider retorna ponto flutuante:

widget.FloatSlider(
       value=5.5, # Valor inicial
       min=-10.0, # Valor mínimo
       max=10.0, # Valor máximo
       step=0.5, # Passo
       description='Decimal:' #Descrição
)

Decimal:

• Checkbox retorna booleano (Verdadeiro ou falso):

widget.Checkbox(
       value=False, # Valor inicial
       description='Booleano', # Descrição
       indent=False # Indentação
)

Booleano:

• Text retorna uma string:

widget.Text(
       value='', # Valor inicial
       placeholder='Digite seu nome', #Nome que aparece quando não escreve nada
       description='Nome: ' # Descrição
)

Nome:

Exemplo 3: Acessando os valores dos Widgets

Toda vez que declaramos um Widget ele inicializa com um valor inicial no parâmetro value.

Por exemplo, digamos que queremos criar um slider chamado em uma célula:

# Célula 1: Declarando o widget chamado Peso
Peso = widget.FloatSlider(
       value=5, # Valor inicial
       min=30, # Valor mínimo
       max=100, # Valor máximo
       step=0.1, # Passo
       description='Peso (kg):' # Descrição
)

E em outra célula mostramos o widget (através da função display()):

# Célula 2: Mostrando o widget
display(Peso)

E na última célula mostramos o resultado:

# Célula 3: Mostrando o valor do Peso
print("O valor do peso é {} kg.".format(Peso.value))

No final o conjunto das três células é a seguinte:

# Célula 1: Declarando o widget chamado Peso
Peso = widget.FloatSlider(
    value=5, # Valor inicial
    min=30, # Valor mínimo
    max=100, # Valor máximo
    step=0.1, # Passo
    description='Peso (kg):' # Descrição
)

# Célula 2: Mostrando o widget
display(Peso)

Peso (kg):

# Célula 3: Mostrando o valor do Peso
print("O valor do peso é {} kg.".format(Peso.value))

O valor do peso é 42.9 kg.

Observe que declaramos o widget em uma célula e mostramos o widget em outra célula. Isso é necessário pois toda vez que você declara um Widget ele sempre inicializa com o valor padrão, desta forma caso o display() esteja na mesma célula toda iteração sera perdida ao executar esta célula novamente.

Atividade 2: Usando Interact

Exemplo 4: Introdução ao interact

Na atividade anterior aprendemos o conceito de Widgets e vimos como eles são úteis para construção de entradas mais elegantes. Porém, a maneira que utilizamos não é eficiente, pois precisavamos interagir o widget e executar a célula seguinte separadamente.

A função interact() permite a criação de widgets de forma muito mais simples do que vimos anteriormente. Além disso, com este método é possível executar o código ao interagir com o widget.

Para trabalhar com o interact() precisamos utilizar os blocos def. No contexto do interact(), os blocos def são um conjunto de instruções que são executadas toda vez que se interage com um widgets.

Os blocos def são trechos de códigos que tem como entrada os argumentos:

def nome_do_bloco(argumento1,argumento2,argumento3,...):
   """
   Instruções do bloco
   """

O interact() associado à este bloco def tem a seguinte notação:

def bloco_def_associado(argumento1,argumento2,argumento3,...):
   # Bloco 1 (Nível 1)
   """
   Instruções do bloco
   """
# Bloco principal (Nível 0)
interact(bloco_def_associado,argumento1=val1,argumento2=val2,...)

Observe que o ìnteract() está no nível 0 e o conteúdo do bloco def está no nível 1.

Para exemplificar o conceito de interact() e blocos def veja o exemplo abaixo:

# Bloco principal (Nível 0)
from ipywidgets import interact
def f(x):
       # Bloco 1 (Nível 0)
       print("O valor de x é {:d}".format(x))
# Bloco principal (Nível 0)
interact(f,#Bloco def que se deseja associar
            x=5 #Variável ou widget
           )

x
O valor de x é 5
<function __main__.f(x)>

Observe também foi imprimido um valor indesejado:

<function __main__.f(x)>

Isso aconteceu porque a função interact retorna o tipo da função <function __main__.f(x)>. Desta forma, a função foi salva na variável _ e imprimida na tela. Veja o que acontece quando mandamos imprimir _

_

<function __main__.f(x)>

Podemos remover essa saída adicionando ; ao final da instrução ìnteract(), assim suprimimos a saída.

# Bloco principal (Nível 0)
from ipywidgets import interact
def f(x):
       # Bloco 1 (Nível 0)
       print("O valor de x é {}".format(x))
# Bloco principal (Nível 0)
interact(f,x=5);

x
O valor de x é 5

Tarefa 2: O tipo de Widget criado pela função ìnteract() depende do tipo de entrada. Repita o exemplo anterior considerando:

• x=2.0
• x=1
• x=True
• x=""
• x="Digite o seu nome"

Exemplo 5: Usando a notação @interact

Utilizando a notação @interact podemos simplificar mais ainda o uso dos Widgets, veja o exemplo abaixo:

@interact(x=5)
def f(x):
    return print("O valor de x é {}.".format(x))

x
O valor de x é 5

Exemplo 6: Abreviações de Widgets

Quando você passa um argumento inteiro, como 5 (x=5) para o interact. A função cria um slider de inteiro no intervalo de $x\in[-5;3\cdot5]$. Neste caso 5 é abreviação de:

IntSlider(min=-5, max=15, step=1, value=5)

De fato, conseguimos o mesmo resultado quando passamos o próprio IntSlider como valor de x:

def f(x):
    print("O valor de x é {}".format(x))
   interact(f,x=widget.IntSlider(min=-5, max=15, step=1, value=5));

x
O valor de x é 5

Ou ainda:

@interact(x=widget.IntSlider(min=-5, max=15, step=1, value=5))
def f(x):
    print("O valor de x é {}".format(x))

x
O valor de x é 5

A tabela abaixo mostra os diferentes tipos de argumentos:

Argumento	Widget
Valor booleano: True ou False	Checkbox
String: "Uma frase" ou ""	Text
Inteiro: valor, (min,max) ou (min,max,passo)	IntSlider
Ponto flutuante: valor, (min,max) ou (min,max,passo)	FloatSlider

Se o segundo parâmetro de interact() for passado como x=(min,max) é produzido um slider com um valor mínimo e máximo com os respectivos valores de min e max. O valor do passo é por padrão 1 e o valor inicial é o meio do intervalo (Considerando o passo).

Por exemplo:

@interact(x=(0,10)) #widget.IntSlider(min=0, max=10)
def f(x):
    print("O valor de x é {}".format(x))

x
O valor de x é 5

E se o terceiro parâmetro for passado como x=(min,max,passo) irá produzir um slider com o valor mínimo, máximo e o passo definido:

@interact(x=(0.0,10.0,0.5))
def f(x):
    print("O valor de x é {}".format(x))

x
O valor de x é 5.0

Tarefa 3: Crie um programa capaz de calcular a área, $A$, e o volume, $V$ de uma esfera. Considere as equações abaixo para fazer o cálculo: \(A=4\pi r^2\)

\[V=\frac{4}{3}\pi r^3\]

O programa deve ter como entrada o raio $r$, que deve ser representado na forma de FloatSlider com valor mínimo de 1, máximo de 10 e passo de 0,1.

A saída deve ser:

r
Com o raio de 5 m a área da esfera é 314.16 m² e o volume é 523.60 m³.

Curiosidade: Existem algumas formas de obter acesso aos dados da função para puder utilizar posteriormente no código.

Observação: Alguns conceitos aqui são avançados, caso tenha dificuldade procure um monitor.

Método 1: Através de variáveis globais

Você pode declarar uma varíavel como global, assim ela é acessível em todo código.

@interact(r=(1,10,0.1))
def calc_esfera(r):
    global A #Com esta diretiva a variável vira global
    global V
    A=4*pi*r**2
    V=4/3*pi*r**3
    print("Com o raio de {:.3g} m a área da esfera é {:.2f} m² e o volume é {:.2f} m³.".format(r,A,V))

r
Com o raio de 5 m a área da esfera é 314.16 m² e o volume é 523.60 m³.

display(A)
display(V)

314.1592653589793
523.5987755982989

Método 2: Através de um dicionário:

from math import pi
import ipywidgets as widget #Importando o pacote com o apelido de widgets
from ipywidgets import interact

Esfera = {} #Criando um dicionário vazio
@interact(r=(1,10,0.1))
def calc_esfera(r):
    Esfera["r"]=r
    Esfera["A"]=4*pi*r**2
    Esfera["V"]=4/3*pi*r**3
    print("Com o raio de {r:.3g} m a área da esfera é {A:.2f} m² e o volume é {V:.2f} m³.".format(**Esfera))

r
Com o raio de 5 m a área da esfera é 314.16 m² e o volume é 523.60 m³.

Esfera

{‘r’: 5.0, ‘A’: 314.1592653589793, ‘V’: 523.5987755982989}

Método 3: Através de uma lista.

Este método é muito parecido com o método 2, ele será apresentado durante a próxima aula!

Exemplo 7: Widgets e gráficos

Para exemplificar o uso dos Widgets vamos apresentar um problema prático de plotagem de gráfico.

Em coordenadas cartesianas as espirais devem utilizar equações paramétricas. A forma geral das espirais no plano cartesiano é:

\[h(\theta)=\begin{cases} x(\theta)=\theta^n\cdot \cos(\theta)\\ y(\theta)=\theta^n\cdot \sin(\theta) \end{cases}\]

Vamos plotar o gráfico de $h(\theta)$ utilizando a função plot_parametric() do pacote sympy (Figura 1):

classDiagram
	sympy .. plotting
	class sympy{
		pi
		symbols()
		cos()
		sin()
	}
	class plotting{
		plot()
		plot_parametric()
	}

Figura 1: Funções do pacote sympy.

O programa vai ter como entrada um Floatslider com $n\in[-2,2]$ e passo $0,1$.

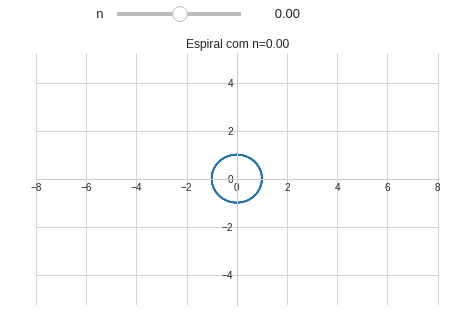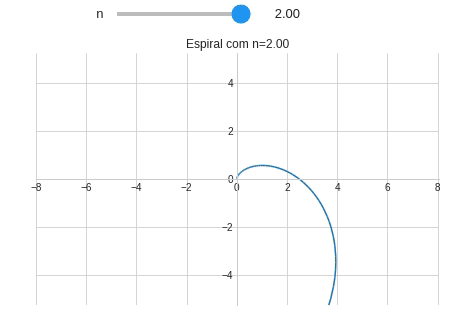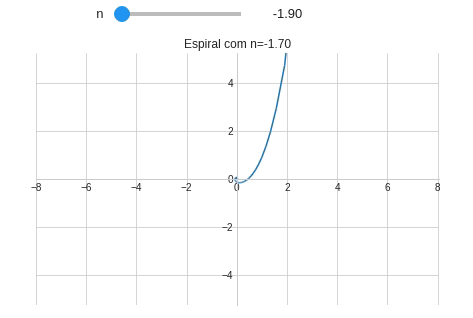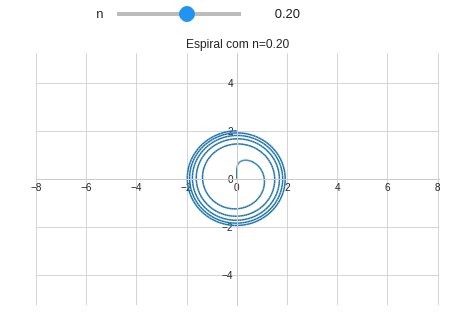
from sympy import symbols, sin, cos, pi #Importando symbols, sin, cos e pi
from sympy.plotting import plot_parametric #Importando plot_parametric

# Definindo um estilo para o gráfico
from matplotlib import style 
style.use('seaborn-whitegrid')


@interact(n=(-2.0,2.0,0.1)) # FloatSlider(min=-2.0,max=2.0,step=0.1)
def plotando_espiral(n):
    theta = symbols('θ')
    x = theta**n*sin(theta)
    y = theta**n*cos(theta)
    plot_parametric(x,y,(theta,0,10*pi),
          xlim=(-8,8.04),
          ylim=(-8.06*15/23,8*15/23), 
          aspect_ratio=(1,1), #Mantendo a proporção de 1:1
          title="Espiral com n={:.2f}".format(n),
          xlabel="",
          ylabel="")

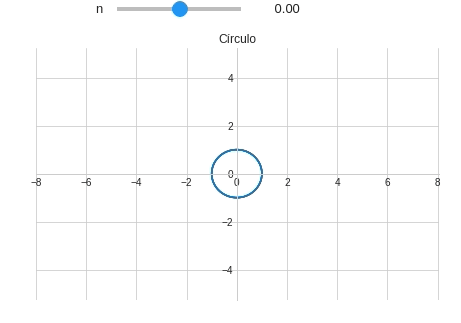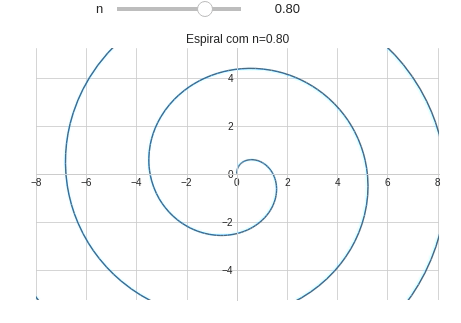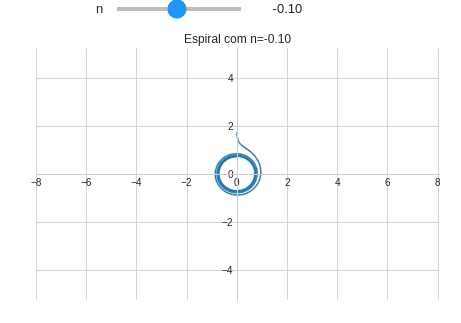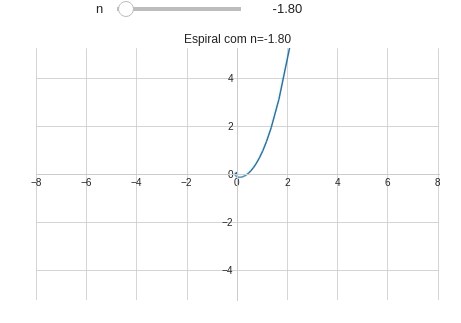
Observe que quando $n=0$ a espiral se reduz à um círculo. Precisamos adicionar este detalhe no nosso programa com ajuda de um if.

@interact(n=(-2,2.0,0.1))
def plotando_espiral(n):
    theta = symbols('θ')
    x = theta**n*sin(theta)
    y = theta**n*cos(theta)
    if n==0:
        título="Círculo"
    else:
        título="Espiral com n={:.2f}".format(n)
    plot_parametric(x,y,(theta,0,10*pi),
          xlim=(-8,8.04),
          ylim=(-8.06*15/23,8*15/23),
          aspect_ratio=(1,1), #Mantendo a proporção de 1:1
          title=título,
          xlabel="",
          ylabel="")

Tarefa 4: Inclinação da reta

Uma reta fixada na origem tem a seguinte notação:

\[f(x)=ax\]

Crie um programa capaz de criar uma reta baseando-se no seu ângulo de inclinação $u$. Para criar a reta utilize a definição de $u$:

\[u=\tan^{-1}(a)\]

ou ainda: \(a=\tan(u)\) Ou resultado da seu código deve ser algo parecido com a Figura abaixo:

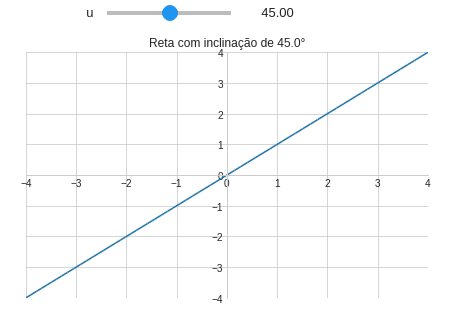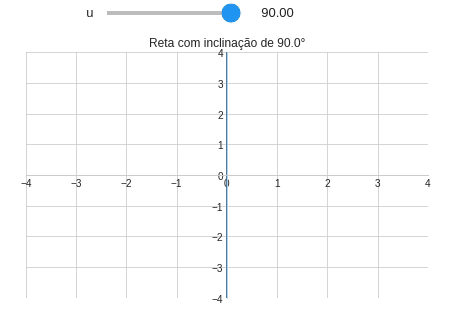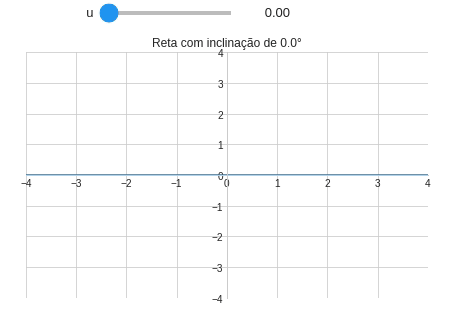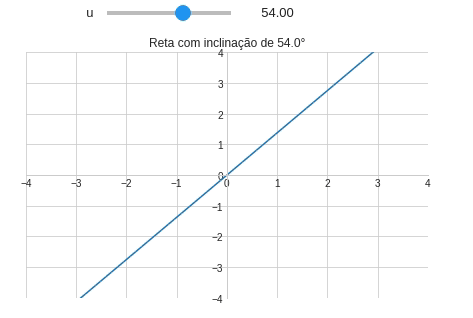
Exemplo 8: Múltiplos argumentos

A função interact() permite trabalhar com múltiplos argumentos, para isto basta associar o bloco def com mais de argumento e adicionar estes argumentos ao interact(). Veja o exemplo abaixo:

@interact(x=(0.0,0.9,0.1),y=(0,3))
   def soma(x,y):
       s=x+y
       print("A soma de {} + {} vale {}".format(x,y,s))

x
y
A soma de 0.4 + 1 vale 1.4

Exemplo 9: Equação da reta

Considerando um exemplo prático, vamos um programa capaz de plotar e escrever a equação da reta no título do gráfico.

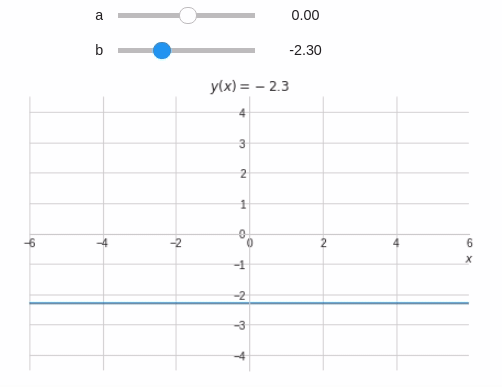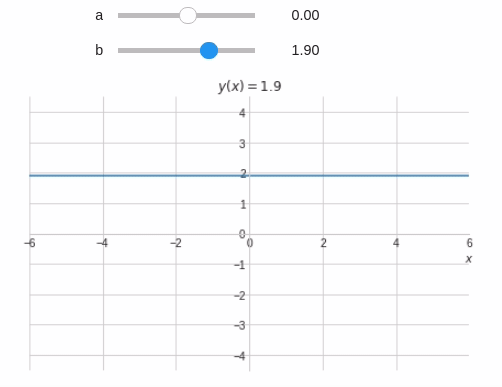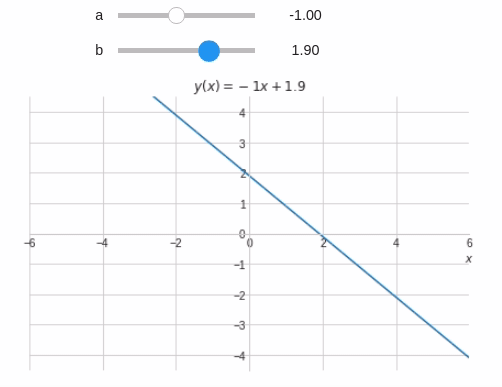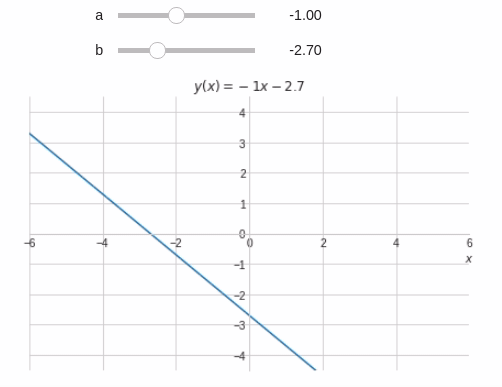
@interact(
       a=widget.FloatSlider(min=-6,max=6,step=0.1,value=1),
       b=(-6,6,0.1) 
)
def eq_reta(a,b):
       x = symbols('x')
       y = a*x+b
       plot(y,(x,-10,10),
                   xlim=(-6,6),
                   ylim=(-6*3/4,6*3/4),
                   title='$y(x)={:.2g}x{:+.2g}$'.format(a,b),
                   xlabel="$x$",
                   ylabel=""
                  )

A equação não é mostrada adequadamente. Vamos corrigí-la utilizando if e concatenação de strings.

A principio vamos seguir as seguintes regras:

• Quando $a=0$ e $b=0$ deve-se $y(x)=0$
• Quando $a=0$ ou $a=1$ deve-se omitir o $a$ na equação
• Quando $a=0$ deve-se omitir $x$ da equação
• Quando $b=0$ deve-se omitir o valor de $b$ na equação
• Quando $a\neq 0$ e $b\neq 0$ deve-se incluir o sinal de $b$

@interact(
       a=widget.FloatSlider(min=-6,max=6,step=0.1,value=1),
       b=(-6,6,0.1)   
)
def eq_reta(a,b):
       x = symbols('x')
       y = a*x+b
       
       # PARCELA 'a'
       if a==1 or a==0:
           a_str = ''
       else:
           a_str = '{:.2g}'.format(a)
            
       # PARCELA 'x'
       if a==0:
           x_str = ''
       else:
           x_str = 'x'
                  
       # PARCELA 'b'
       if b==0:
           if a==0:
               b_str = '0'
           else:
               b_str = ''
       elif a!=0: #Quando a é diferente de zero deve-se incluir o '+'
           b_str = '{:+.2g}'.format(b)
       else: #Quando a é zero não é necessário incluir o '+'
           b_str = '{:.2g}'.format(b)
       
       # Escrevendo a equação
       t = '$y(x)=' + a_str + x_str + b_str +'$'
       
       plot(y,(x,-10,10),
                   xlim=(-6,6),
                   ylim=(-6*3/4,6*3/4),
                   title=t,
                   xlabel="$x$",
                   ylabel=""
                  )

Podemos simplificar um pouco o nosso programa se utilizarmos a variavel $t$ como um acomulador:

@interact(
       a=widget.FloatSlider(min=-6,max=6,step=0.1,value=1),
       b=(-6,6,0.1)
)
def eq_reta(a,b):
       x = symbols('x')
       y = a*x+b
       t = '$y(x)='
       
       # PARCELA 'a'
       if a!=1 and a!=0:
           t+= '{:.2g}'.format(a) #t=t+'{:.2g}'.format(a)
            
       # PARCELA 'x'
       if a!=0: 
           t+= 'x' #t=t+x
                  
       # PARCELA 'b'
       if b==0:
           if a==0:
               t+= '0'
       elif a!=0:
           t+= '{:+.2g}'.format(b)
       else:
           t+= '{:.2g}'.format(b)  
       
       # Finalizando
       t += '$'
       
       plot(y,(x,-10,10),
                   xlim=(-6,6),
                   ylim=(-6*3/4,6*3/4),
                   title=t,
                   xlabel="$x$",
                   ylabel=""
                  )

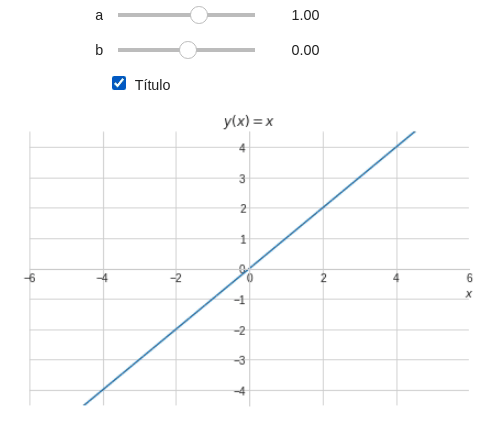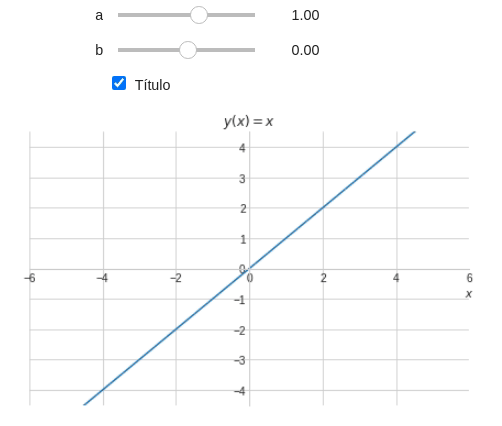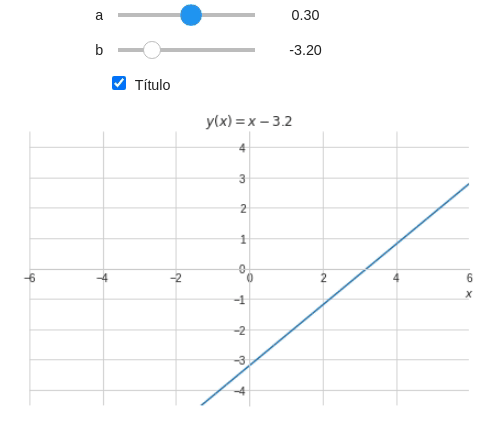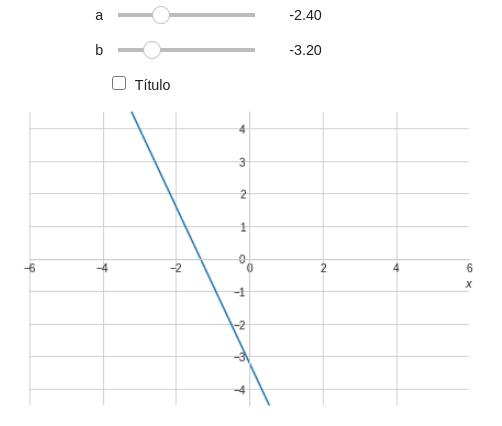
Finalmente, vamos adicionar a posssiblidade do usuário mostrar ou esconder a equação (o título):

@interact(
       a=widget.FloatSlider(min=-6,max=6,step=0.1,value=1),
       b=(-6,6,0.1),
       Título=True 
)
def eq_reta(a,b,Título):
       x = symbols('x')
       y = a*x+b
       t = '' #Inicio o t como uma string vazia
       
       #Vou adicionando termos às strings a medida que passa pelos ifs
       if Título:
           t += '$y(x)=' 

           # PARCELA 'a'
           if a!=1 and a!=0:
               t+= '{:.2g}'.format(a)

           # PARCELA 'x'
           if a!=0: 
               t+= 'x'

           # PARCELA 'b'
           if b==0:
               if a==0:
                   t+= '0'
           elif a!=0:
               t+= '{:+.2g}'.format(b)
           else:
               t+= '{:.2g}'.format(b)  

           # Finalizando
           t += '$'
       
       plot(y,(x,-10,10),
                   xlim=(-6,6),
                   ylim=(-6*3/4,6*3/4),
                   title=t,
                   xlabel="$x$",
                   ylabel=""
                  )

Tarefa 5: Modifique o exemplo da espiral considerando as seguintes premissas:

• Adicione a possiblidade de mostrar e ocultar o título e os eixos;
• Nomei os eixos como $x$ e $y$;
• Adicione a possibilidade de escolher a cor do gráfico utilizando o Widget ColorPicker. Utilize os parâmetros description="Cor:" e value="green" (Veja a documentação);
• Use o parâmetro line_color (Na função print) para alterar a cor do gráfico.

A sua saída do programa deve ser parecida com essa:

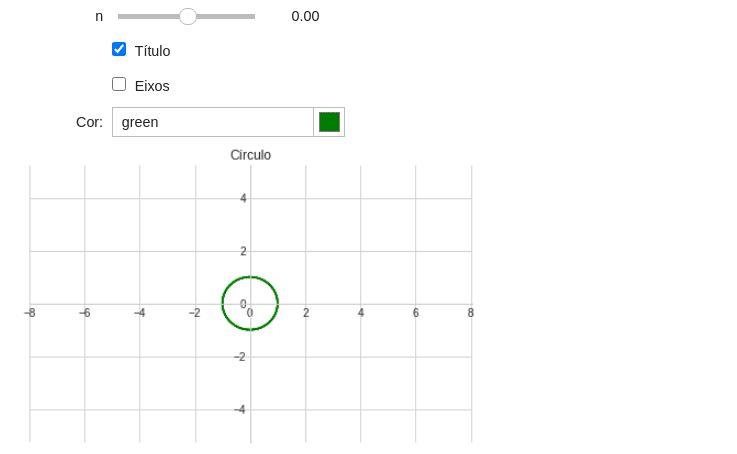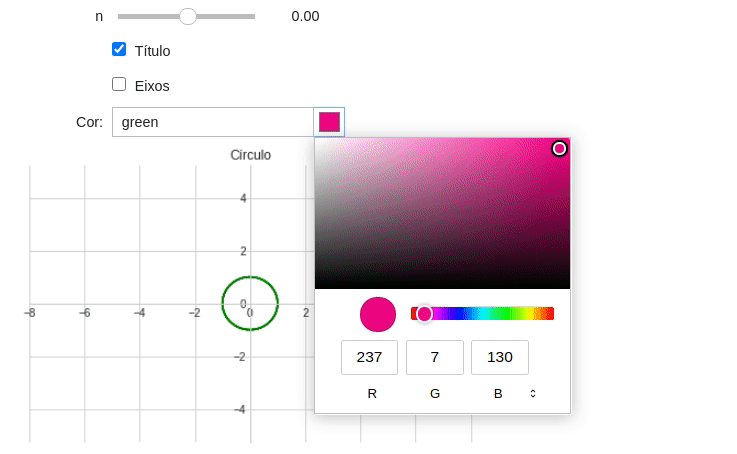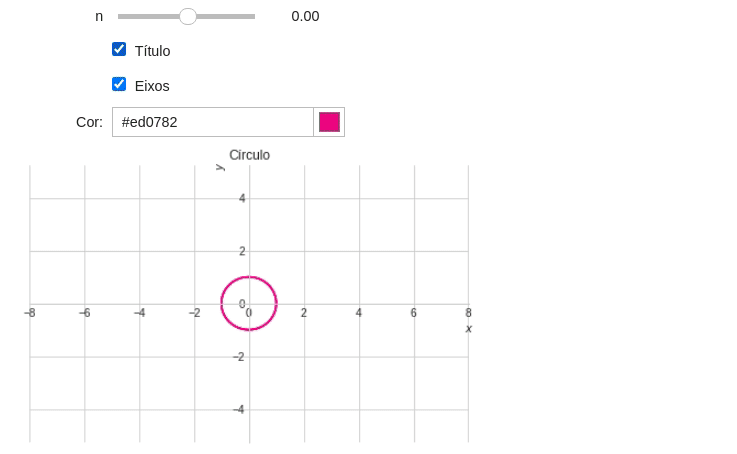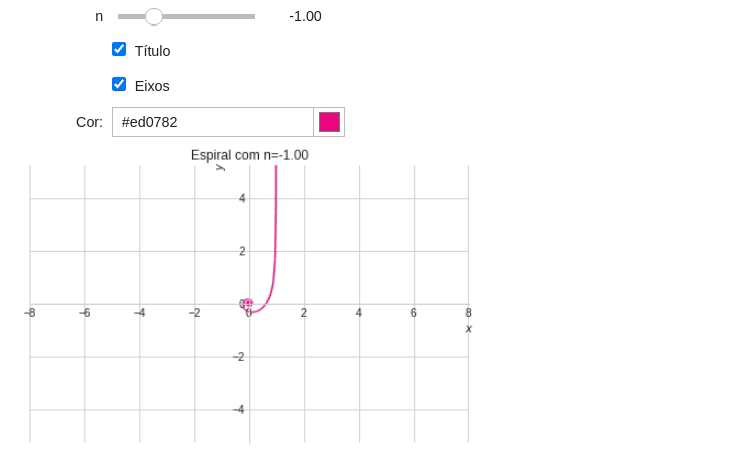
Exemplo 10: Widgets e configurações de plotagem

Por padrão o módulo sympy.plotting utiliza o algoritmo adaptativo para calcular o número de pontos do gráfico. Este algoritmo calcula o número de pontos de cada área do gráfico de forma ter um gráfico sem ‘defeitos’,entretanto este algoritmo não é preciso para algumas funções. Neste caso, é interessante selecionar o número de pontos manualmente através do atributo nb_of_points. O parâmetro adaptive determina se o algoritmo adaptativo é utilizado ou não:

• adaptive=True $\rightarrow$ O algoritmo adaptativo é ativado (Valor padrão)
• adaptive=False $\rightarrow$ Utiliza um determinado número de pontos igualmente espaçados. Este número é determinado pelo parâmetro nb_of_points

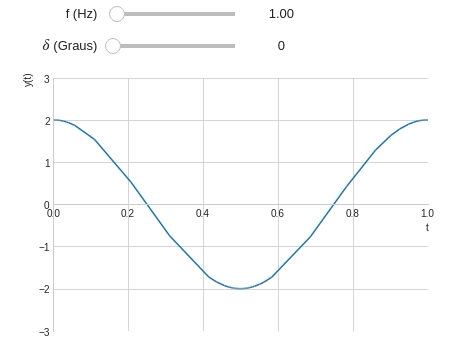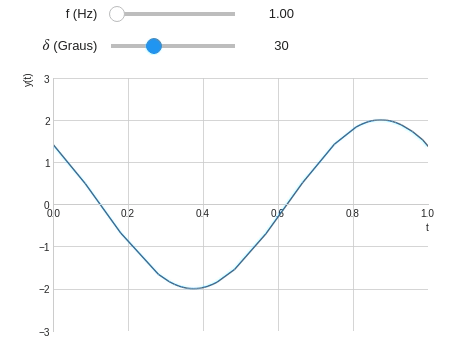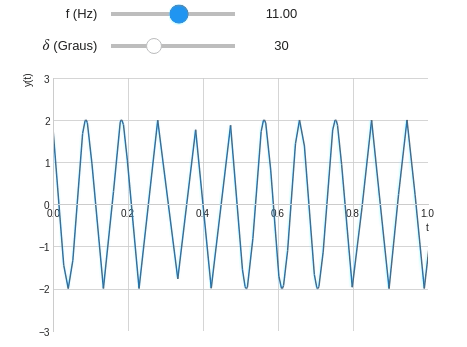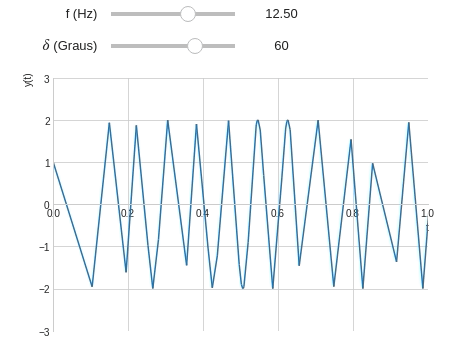
Para exemplificar o uso deste dois parâmetros de configuração de plotagem vamos considerar um exemplo de uma onda seinodal:

\[y(t)=2\cos(2\pi f t+\delta)\]

onde o usuário controla a frequência da onda $f$.

Além disso, vamos adicionar a possiblidade de o usuário escolher o algoritmo de plotagem (adaptive True ou False) e o número de pontos do gráfico, caso o algoritmo adaptativo esteja desativado.

Inicialmente vamos construir o gráfico da onda sem essa possibilidade de customização de plotagem.

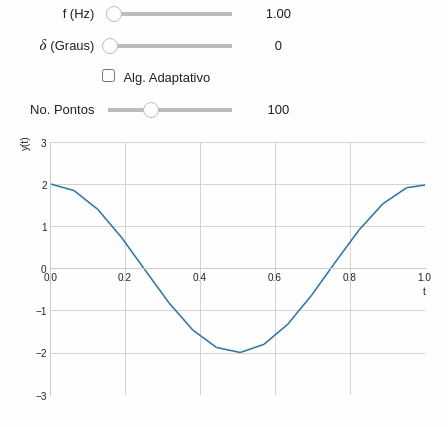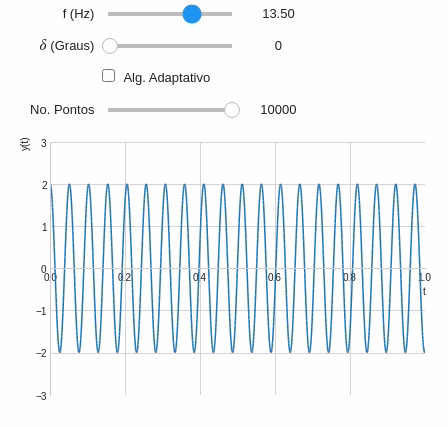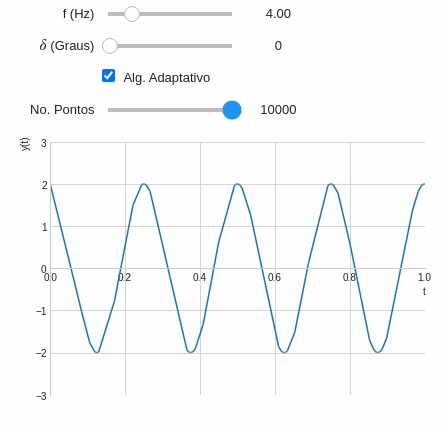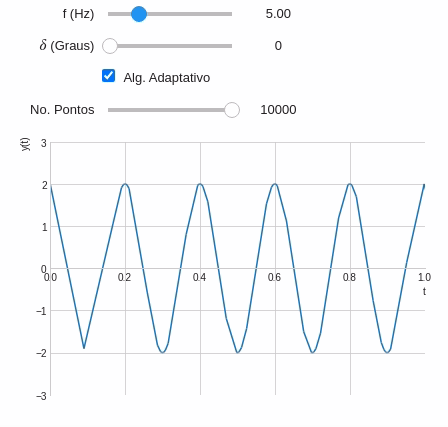
@interact(
    # Frequência variando entre 0,2 e 20 Hz 
    f=widget.FloatSlider(min=0.5,max=20,step=0.5,value=1,description='f (Hz)'),
    # Fase variando entre 0 e 90°
    d=widget.IntSlider(min=0,max=90,step=15,description="$\delta$ (Graus)")
) 
def plot_onda(f,d):
    t=symbols('t')
    y=2*cos(2*pi*f*t+radians(d))
    plot(y,(t,0,2*pi),
         ylim=(-3,3),
         xlim=(0,1),
         ylabel='y(t)'
        )

Observe que a precisão de plotagem diminui quando a frequência da onda aumenta. Isso acontece pois o número de pontos (ou amostras) não são o suficiente para representar o gráfico com fidelidade. Podemos corrigir isso através configurando o número de pontos manualmente.

Agora vamos adicionar a possiblidade do usuário escolher a configuração de plotagem de acordo com as regras abaixo:

• adaptive=True $\rightarrow$ O algoritmo adaptativo é ativado (Valor padrão)
• adaptive=False $\rightarrow$ Utiliza um determinado número de pontos igualmente espaçados. Este número é determinado pelo parâmetro nb_of_points

@interact(
    # Frequência variando entre 0,2 e 20 Hz 
    f=widget.FloatSlider(min=0.5,max=20,step=0.5,value=1,description='f (Hz)'),
    # Fase variando entre 0 e 90°
    d=widget.IntSlider(min=0,max=90,step=15,description="$\delta$ (Graus)"),
    alg=widget.Checkbox(description='Alg. Adaptativo',value=False),
    
    #Vamos utilizar o FloatLogSlider
    pts=widget.FloatLogSlider(
        description='No. Pontos',
        min=1, #Expoente mínimo
        max=4, #Expoente máximo
        value=1e2, #Valor inicial
        base=10, #Base (O número dobra a cada passo)
        step=1, #Passo
        readout_format='d' #Mostrando a saída na forma de inteiro
    )
) 
def plot_onda(f,d,alg,pts):
    t=symbols('t')
    y=2*cos(2*pi*f*t+radians(d))
    plot(y,(t,0,2*pi),
         ylim=(-3,3),
         xlim=(0,1),
         ylabel='y(t)',
         adaptive=alg,
         nb_of_points=int(pts)
        )

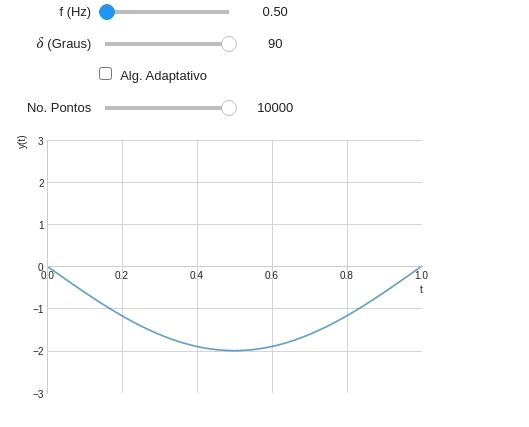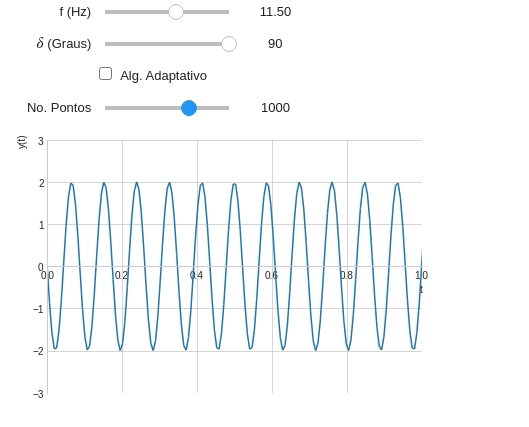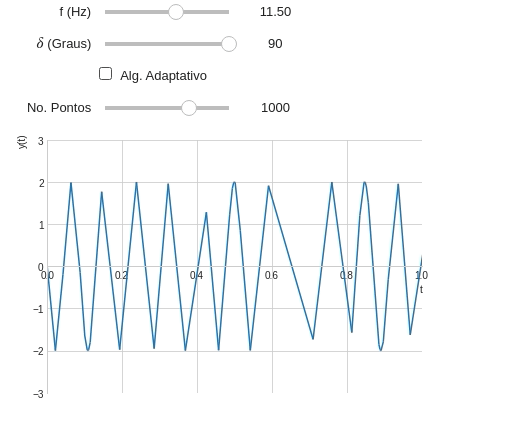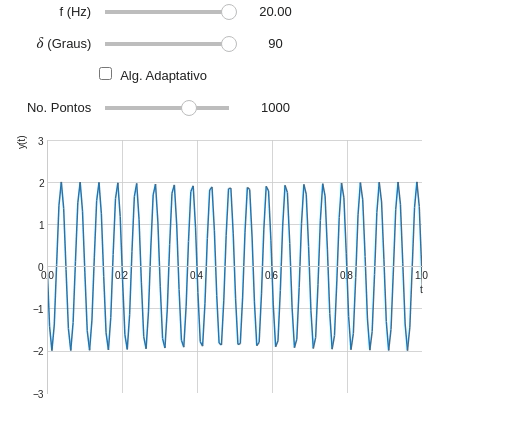
Quando o algoritmo adaptativo está habilitado o número de ponto não tem efeitos. Sendo assim, vamos desativar o widget que controla o número de pontos:

ptWidget=widget.FloatLogSlider(
        description='No. Pontos',
        min=1, #Expoente mínimo
        max=4, #Expoente máximo
        value=1e2, #Valor inicial
        base=10, #Base (O número dobra a cada passo)
        step=1, #Passo
        readout_format='d' #Mostrando a saída na forma de inteiro
)

@interact(
    # Frequência variando entre 0,2 e 20 Hz 
    f=widget.FloatSlider(min=0.5,max=20,step=0.5,value=1,description='f (Hz)'),
    # Fase variando entre 0 e 90°
    d=widget.IntSlider(min=0,max=90,step=15,description="$\delta$ (Graus)"),
    alg=widget.Checkbox(description='Alg. Adaptativo',value=False),
    #Vamos utilizar o FloatLogSlider
    pts=ptWidget
) 
def plot_onda(f,d,alg,pts):
    t=symbols('t')
    y=2*cos(2*pi*f*t+radians(d))
    ptWidget.disabled=alg # Se o método adataptativo estiver ativado desativa o widget
    plot(y,(t,0,2*pi),
         ylim=(-3,3),
         xlim=(0,1),
         ylabel='y(t)',
         adaptive=alg,
         nb_of_points=int(pts)
        )

Atividade 3: Interact_manual()

O interact_manual() é uma variação do interact que permite a execução do código apenas quando se clica em um determinado botão. Isso é especialmente útil quando o bloco def tem instruções muito demoradas ou quando o você não quer executar o bloco def imediatamente após a iteração do widget. Para exemplificar refazemos o exemplo da soma usando o ìnteract_manual():

from ipywidgets import interact_manual
@interact_manual(x=(0.0,0.9,0.1),y=(0,3))
def soma(x,y):
    s=x+y
    print("A soma de {} + {} vale {}".format(x,y,s))

Agora vamos para um exemplo prático.

Exemplo 10: Número Primo

Um número é primo quando ele somente é divisível por um e por ele mesmo. Podemos criar um algoritmo que utiliza a força bruta para encontrar números primos. Neste programa vamos dividir o número por todos os divisores possíveis entre 2 e o “Número/2”.

Observação: Acima de “Número/2” não há divisores para este número, por isso buscar por divisores acima disso é um desperdício de energia.

graph TB
    idi((Início)) --> id2
    id2[Divida o <b>Número</b> por todos os números entre <b>2</b> e o <b>Número/2</n>] --> idp
    idp{O <b>Número</b> é divisível por esses números?} -- True --> id3[Não é primo] --> idf((Fim))
    idp -- False --> id4[É primo] --> idf

Para testar o nosso programa podemos utilizar alguns números primos da lista abaixo:

Os primeiros 25 números primos são:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97

Números primos grandes:

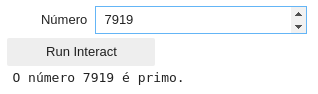
7919, 27644437

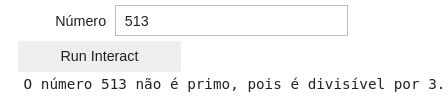
@interact_manual(Número="")
def checar_primo(Número):
    if not(Número.isdigit()):
        print("Por favor digite um número inteiro e positivo!")      
    else:
        Número=int(Número) # Converte o número para inteiro          
        divisor = 2
        primo = True # Iniciamos com a suposição que o número é primo
        
        while (divisor<= Número/2):
            if (Número % divisor == 0): # Se o resto for 0 ele é divisível
                primo=False # Se ele for divisível ele não é primo
                break # Saia do loop para economizar processamento
            divisor+=1 # Essa expressão tem o mesmo valor que divisor = divisor +1
         
        if primo:
            print("O número {} é primo.".format(Número))
        else:
            print("O número {} não é primo, pois é divisível por {}.".format(Número,divisor))

Observação: A tarefa de encontrar números primos grandes é demasiadamente demorada, este é um exemplo perfeito para a utilização do interact_manual().

No exemplo acima conseguimos garantir que o número digitado seja primo utilizando o método .isdigit(). Contudo, podemos resolver este problema apenas com os Widgets.

Existem Widgets de texto que permitem trabalharmos somente com números. Alguns deles permitem limitar os intervalos. São eles:

Widget	Função
IntText	Inteiro (Sem limitação)
FloatText	Ponto flutuante (Sem limitação)
BoundedIntText	Inteiro (Limitado)
BoundedFloatText	Ponto flutuante (Sem limitação)

No nosso caso iremos utilizar o Widget BoundedIntText que permite somente números inteiros, limitados a um intervalo.

@interact_manual(Número=widget.BoundedIntText(min=0,max=27644437))
def checar_primo(Número):     
    divisor = 2
    primo = True # Iniciamos com a suposição que o número é primo
      
    while (divisor<= Número/2):
        if (Número % divisor == 0): # Se o resto for 0 ele é divisível
            primo=False # Se ele for divisível ele não é primo
            break # Saia do loop para economizar processamento
        divisor+=1 # Essa expressão tem o mesmo valor que divisor = divisor +1
         
    if primo:
        print("O número {} é primo.".format(Número))
    else:
        print("O número {} não é primo, pois é divisível por {}.".format(Número,divisor))

Consideramos incluir as exceções a regra:

• O número 1 não é primo, pois tem um único divisor;
• 0 não é primo, pois um número divido por zero é indeterminado;

@interact_manual(Número=widget.BoundedIntText(min=0,max=27644437))
def checar_primo(Número):  
       if(Número>1):
           divisor = 2
           primo = True # Iniciamos com a suposição que o número é primo
   
           while (divisor<= Número/2):
               if (Número % divisor == 0): # Se o resto for 0 ele é divisível
                   primo=False # Se ele for divisível ele não é primo
                   break # Saia do loop para economizar processamento
               divisor+=1 # Essa expressão tem o mesmo valor que divisor = divisor +1
   
           if primo:
               print("O número {} é primo.".format(Número))
           else:
               print("O número {} não é primo, pois é divisível por {}.".format(Número,divisor))
       elif (Número==1):
           print("O número 1 não é primo, pois tem apenas um único divisor.")
       else:
           print("O número 0 não é primo, pois divisão por 0 é indeterminada.")

Tarefa 6: Crie um programa capaz de reverter a ordem de impressão de um número:

• Use um widget de campo de texto como entrada;
• O programa deve aceitar somente números inteiros e positivos;
• Você deve trabalhar com o número (E não com a string).

Se precisar, você pode copiar e colar o seguinte diagrama numa célula Markdown para te ajudar.

​```mermaid
flowchart TB
    idi((Início)) --> id1["Assuma que <b>NumRevertido</b> é 0"] --> idp
    idp{"<b>Número</b> == 0?"} -- False --> id3
    id3["Calcule o <b>Resto</b> do <b>Número</b> dividido por 10"] --> id4
    id4[Multiplique <b>NumRevertido</b> por 10 e some com o <b>Resto</b>] --> id5
    id5[Divisão inteira do <b>Número</b> por 10] --> idp
    idp -- True --> idf((Fim))
​```

Atividade 4: Para casa

Exercício 1: Parábola

Uma parábola tem a sua função dada por:

\[f(x)=ax^2+bx+c\]

De forma similar à tarefa da equação da reta crie um programa capaz de criar um gráfico de uma equação do segundo grau. Considere as seguintes premissas:

• Os valores de $a$, $b$ e $c$ devem ser entradas do programa na forma de Sliders;
• Os sliders devem ter os seguintes parâmetros:

Slider	Min	Max	Passo	Val. Inicial
a	-2.0	2.0	0.05	0.25
b	-20.0	20.0	0.5	0.0
c	-45.0	45.0	0.5	0.0

• O título do gráfico deve mostrar a equação da parábola (Considere mostrar a equação correntamente, considerando as situações que $a$, $b$ e/ou $c$ podem ser zero ou que $a$ e/ou $b$ podem ser 1);
• O usuário poderá alterar a cor do gráfico através de um Widget;
• Os limites do gráfico devem ser $x\in[-100,100]$ e $f(x)\in[-200,200]$;
• O usuário pode mostrar ou ocultar o título;
• O usuário pode escolher o algoritmo de plotagem (Uso do algoritmo adaptativo);
• Caso o usuário não escolha o algoritmo adaptativo, o mesmo poderá escolher a quantidade de pontos através de um FloatLogSlider:

Características	Valor
base	2
min	64 pontos
max	4096 pontos

• Você deve utilizar $x$ como variável simbólica;
• O gráfico deve ser plotado com a função plot() do pacote sympy.

O resultado do seu programa deve ser parecido com a imagem abaixo:

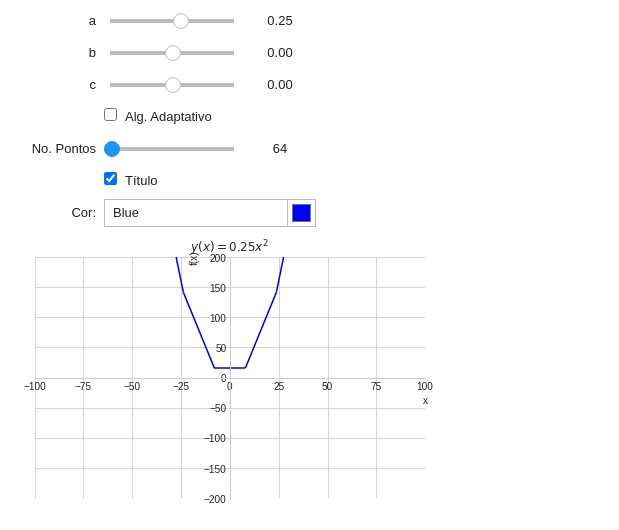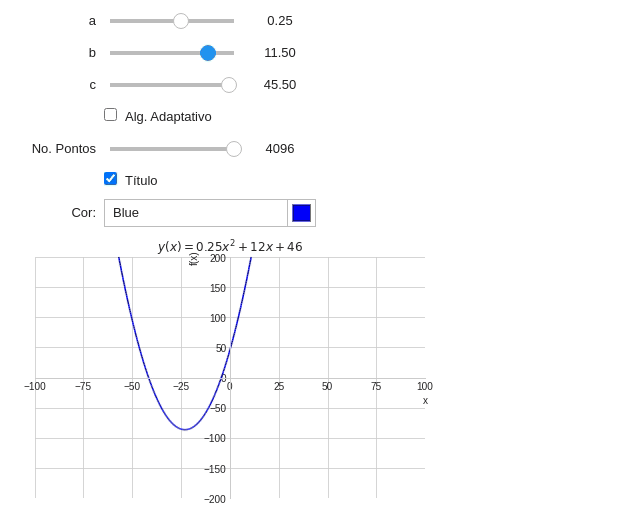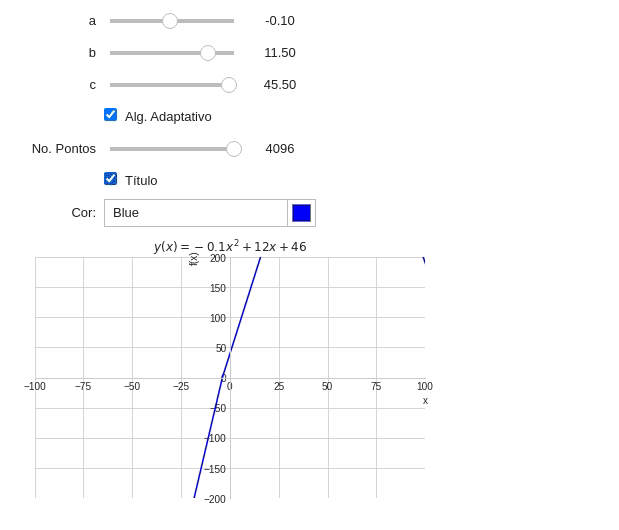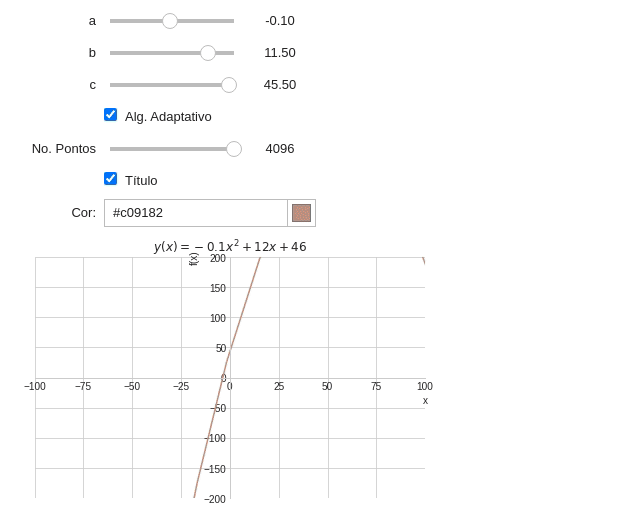Teste seu exemplo e discuta as vantagens e desvantagens do algoritmo adaptativo.

Exemplo 2: Dissecando uma string

Faça um programa que tenha como entrada uma caixa de texto (o Widget Textarea). O programa deve analisar o conteúdo da caixa de texto e verificar se:

• O texto só tem espaços;
• O texto está vazio;
• O texto é numérico;
• O texto é alfabético;
• O texto é alfanumérico;
• O texto pode ser utilizado como um identificador padrão do Python;
• O texto está em maiúsculas;
• O texto está na forma de título;
• O texto está em minúsculas.

Você deve pesquisar sobre o Widget Textarea na documentação.

A análise do texto deve ser feita em tempo real.

O resultado do seu programa deve ser parecido com a imagem abaixo:

Exemplo 3: Contando dígitos

Crie um programa capaz de contar a quantidade de dígitos de um número inteiro.

• Use um widget de campo de texto como entrada;
• O programa deve aceitar qualquer número inteiro (Positivos e negativos).

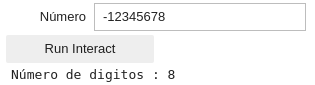
Exemplo 4: Divisores de um número

Crie um programa capaz de encontrar todos os divisores de um número.

• Use um widget de campo de texto como entrada;
• O programa deve aceitar somente números inteiros entre 0 e 500.

O usuário deve clicar num botão para fazer a análise do número (Use o interact_manual).

O resultado do seu programa deve ser parecido com a imagem abaixo:

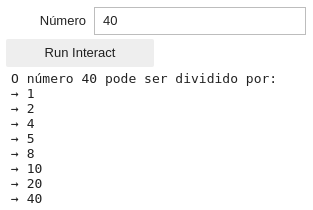
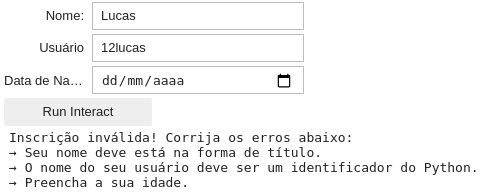
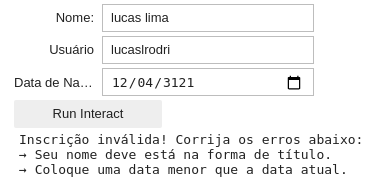
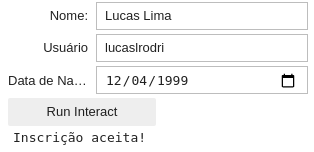
Exemplo 5: Formulário

Crie um programa que capaz de fazer a inscrição de um determinado usuário. O formulário deve ter como entrada:

• Nome (Só aceita se a string for na forma de título e não for na forma alfanumérica)
• Nome do usuário (Só aceita se aceita se a string for um identificador padrão do Python)
• Data de nascimento (Só aceita se o usuário for maior de 18 anos) (Utilize o widget DatePicker)

Para aceitar a inscrição o usuário deve clicar num botão (Use o interact_manual).

Caso a inscrição for inválida o programa deve indicar a causa do erro. Caso a inscrição seja válida o programa deve imprimir:

Inscrição validada com sucesso!

Use o módulo datetime e a função abaixo para te ajudar a construir o seu programa:

from datetime import date

def calcularIdade(dataNascimento):
    """
    Esta função retorna a sua idade de acordo com a data de nascimento
    A função retorna 'Erro' caso a data de nascimento não for definida
    """
    try:
        hoje = date.today() #Captura a data de hoje
    
        # Calcula a sua idade baseando-se na:

        ## Diferença dos anos
        idade = hoje.year - dataNascimento.year

        ## Diferença entre os meses de aniversário
        if (hoje.month, hoje.day) < (dataNascimento.month, dataNascimento.day):
            idade -= 1

        return idade #Retorna a sua idade como valor de saída
    except AttributeError:
        return "Erro" #Em caso de erro retorna 'Erro'

O resultado do seu programa deve ser parecido com as imagens abaixo: